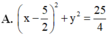
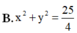
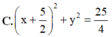
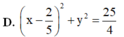
Tập hợp tất cả các điểm biểu diễn số phức z thỏa mãn điều kiện z - i = 2 - 3 i - z là
A. Một đường tròn.
B. Một đường Elip.
C. Một đường thẳng.
D. Một đoạn thẳng.
Tập hợp tất cả các điểm biểu diễn số phức z thỏa mãn điều kiện z - i = 2 - 3 i - z là
A. Một đường tròn
B. Một đường Elip.
C. Một đường thẳng.
D. Một đoạn thẳng.
Chọn C.
Phương pháp: Biến đổi đẳng thức đã cho.
Cách giải: Giả sử
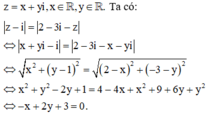
Vậy tập hợp tất cả các điểm biểu diễn số phức z thỏa mãn điều kiện z - i = 2 - 3 i - z là một đường thẳng.
Tìm tập hợp các điểm biểu diễn số phức z trên mặt phẳng tọa độ thỏa mãn các điều kiện: |2 + z| < |2 – z|
Ta có: | 2 + z | 2 < | 2 - z | 2
⇔ | 2 + x + iy | 2 < | 2 - x - iy | 2
⇔ 2 + x 2 + y 2 < 2 - x 2 + - y 2
⇔ x < 0
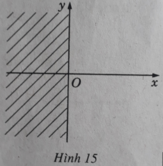
Đó là tập hợp các số phức có phần thực nhỏ hơn 0, tức là nửa trái của mặt phẳng tọa độ không kể trục Oy.
Trên mặt phẳng Oxy, tập hợp các điểm biểu diễn số phức z thỏa mãn điều kiện z - 2 + z + 2 = 6 là
B. Đường thẳng y = 6.
D. Đường tròn tâm (0;2), bán kính bằng 6
Trên mặt phẳng Oxyz tập hợp các điểm biểu diễn số phức z thỏa mãn điều kiện z - 2 + z + 2 = 6 là
A. E l í p x 2 9 + y 2 5 = 1
B. Đ ư ờ n g t h ẳ n g y = 6
C. ( 0 ; 2 ) , ( 0 ; - 2 )
D. Đ ư ờ n g t r ò n t â m ( 0 ; 2 ) b á n k í n h b ằ n g 6
Cho số phức z thỏa mãn điều kiện: z − 1 = z + 3 − 2 i . Tập hợp các điểm biểu diễn số phức z là
A. Đường thẳng
B. Đường tròn
C. Một điểm xác định
D. Elip
Đáp án A
Em hãy thực hiện câu này theo cả 2 cách nhé!
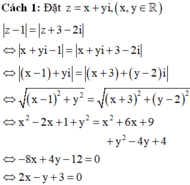
Vậy tập hợp các điểm biểu diễn số phức z là một đường thẳng có phương trình: 2x - y + 3 = 0
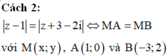
Em thấy, điểm M cách đều hai điểm A, B nên M thuộc đường trung trực của đoạn thẳng AB.
Em có thể tìm phương trình đường trung trực ∆ của đoạn thẳng AB như sau:
AB → = − 4 ; 2 , trung điểm của AB là I − 1 ; 1 , ∆ qua điểm I nhận AB → = − 4 ; 2 làm vectơ pháp tuyến.
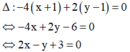
Cho số phức z thỏa mãn điều kiện: |z-1| = |z+3-2i|. Tập hợp các điểm biểu diễn số phức z là
A. Đường thẳng.
B. Đường tròn.
C. Một điểm xác định.
D. Elip.
Đáp án A
Em hãy thực hiện Câu nay theo cả 2 cách nhé!
Cách 1: Đặt 
Cách 2: 
với M(x;y), A(1;0) và B(-3;2)
Em thấy, điểm M cách đều hai điểm A, B nên M thuộc đường trung trực của đoạn thẳng AB.
Em có thể tìm phương trình đường trung trực ∆ của đoạn thẳng AB như sau:
trung điểm của AB là I(-1;1),
∆
qua điểm I nhận 
làm vectơ pháp tuyến.
Trên mặt phẳng tọa độ Oxy, tìm tập hợp các điểm biểu diễn các số phức z thỏa mãn điều kiện |z – 2| + |z + 2| = 10.
A. Đường tròn ( x - 2) 2 + ( y + 2) 2 = 100.
B. Elip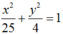 
C. Đường tròn ( x -2) 2 + ( y + 2) 2 = 10.
D. Elip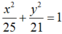 
Chọn D.
Gọi M(x; y) là điểm biểu diễn số phức z = x + yi, x, y ∈ R
Gọi A là điểm biểu diễn số phức 2
Gọi B là điểm biểu diễn số phức -2
Ta có: |z – 2| + |z + 2| = 10 ⇔ MB + MA = 10.
Ta có AB = 4.
Suy ra tập hợp điểm M biểu diễn số phức z là Elip với 2 tiêu điểm là A(2; 0), B( -2; 0) tiêu cự AB = 4 = 2c, độ dài trục lớn là 10 = 2a , độ dài trục bé là 
Vậy tập hợp các điểm biểu diễn các số phức z thỏa mãn điều kiện |z – 2| + |z + 2| = 10 là elip có phương trình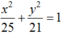 
Xét các số phức z thỏa mãn điều kiện z - 1 + i = 2 Trong mặt phẳng tọa độ Oxy, tập hợp các điểm biểu diễn các số phức w = z + 2 -i là
A. đường tròn tâm I(-3;2), bán kính R = 2.
B. đường tròn tâm I(3;-2), bán kính R = 2.
C. đường tròn tâm I(1;0), bán kính R =2.
D. đường tròn tâm I(1;-1), bán kính R = 2.
Xét các số phức z thỏa mãn điều kiện |z-3+2i|=5. Trong mặt phẳng tọa độ Oxy, tập hợp của điểm biểu diễn số phức z là
A.Đường tròn tâmI(3;-2),bán kính R=5
B.Đường tròn tâm I(-2;1), bán kính R=5
C.Đường tròn tâm I(4;-3),bán kính R=5.
D. Đường tròn tâm I(-4;3), bán kính R=5
