a) Kéo dài các tia AN; AE; AM; AF cho chúng cắt đường thẳng BC theo thứ tự tại các điểm G;H;I;K.

Xét \(\Delta\)ABI có: BM  là phân giác ^ABI và BM vuông góc AI (tại M) => \(\Delta\)ABI cân tại B

=> BM đồng thời là đường trung tuyến \(\Delta\)ABI => M là trung điểm AI

C/m tương tự, ta có: N;E;F lần lượt là trung điểm của AG;AH;AK

Xét \(\Delta\)GAH: N là trung điểm AG; E là trung điểm AH => NE là đường trung bình \(\Delta\)GAH

=> NE // GH hay NE // BC (1)

Tương tự: MF // BC (2);  NF // BC (3)

Từ (1); (2) và (3) => 4 điểm M;N;E;F thẳng hàng (Theo tiên đề Ơ-clit) (đpcm).

b) Theo câu a ta có: NF là đường trung bình \(\Delta\)AGK => \(NF=\frac{GK}{2}=\frac{BG+BC+CK}{2}\)(*)

Lại có: \(\Delta\)ABG cân ở B; \(\Delta\)ACK cân ở C (câu a) nên BG = AB; CK = AC

Thế vào (*) thì được: \(NF=\frac{AB+BC+AC}{2}\),

KL: ...

a/ Vì BM và CQ lần lượt là tia phân giác ngoài của các tia phân giác trong góc B,C nên góc MBN = góc PCQ = 90 độ

Xét tam giác AEN và tam giác BEM có AE = EB ; góc BEM = góc AEN (đối đỉnh) , góc MBE = góc EAN (cùng phụ góc ABN)

=> Tam giác AEN = tam giác BEM (c.g.c) => EM = EN 

Suy ra AMBN là hình bình hành vì tứ giác này có hai đường chéo cắt nhau tại trung điểm mỗi đường

Mà có một góc bằng 90 độ => AMBN là hình chữ nhật

Chứng minh tương tự với tứ giác APCQ

b/ Dễ dàng chứng minh được EF là đường trung bình tam giác ABC => EF // BC (1)

Vì AMBN là hình chữ nhật mà E là giao điểm của hai đường chéo nên M,E,N thẳng hàng (2)

Tương tự APCQ là hình chữ nhật nên P,F,Q thẳng hàng (3)

Theo tính chất hình chữ nhật thì góc ENB góc EBN = góc NBC => MN // BC (4)

Tương tự, ta có PQ // BC (5)

Từ (1) , (2) , (3) , (4) , (5) suy ra M,N,P,Q,E,F thẳng hàng. (Áp dụng tiên đề Ơ-clit)

jygvk

M,N,P,Q,E,F thẳng hàng

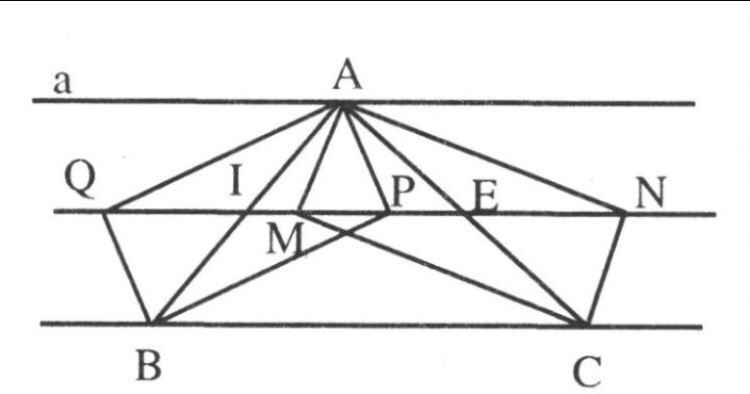
a. Vì BQ và BP là p/g ngoài và trong của \(\widehat{ABC}\) nên \(BP\bot BQ\)

Lại có \(AQ\bot BQ, AP\bot BP\) nên AQPB là hcn

Cmtt ta được AMCN cũng là hcn

b. Gọi I là giao 2 đường chéo AB và PQ của hcn AQBP

\(\Rightarrow IB=IA=IC\\ \Rightarrow\widehat{IPB}=\widehat{IBP}=\widehat{PBC}\left(BP\text{ là p/g}\right)\)

Mà 2 góc này ở vị trí slt nên IP//BC

\(\Rightarrow P,Q\) nằm trên đtb của \(\Delta ABC\)

Tương tự M,N cũng nằm trên đtb \(\Delta ABC\)

Vậy M,N,Q,P thẳng hàng

HN//AB

=>góc NHA=góc HAM

=>góc NHA=góc MHA

=>HA là phân giác của góc NHM

HC vuông góc HA

=>HC là phân giác ngoài của ΔIHN

a. Do hai đường phân giác trong và ngoài của góc B vuông góc với nhau nên AMBN là hình chữ nhật (Tứ giác có 3 góc vuông)

Tương tự ACPQ cũng là hình chữ nhật.

b. Do câu a, AMBN là hình chữ nhật nên MN và BA cắt nhau tại trung điểm mỗi đường. Vì thế M, N, E thẳng hàng. Tương tự P, F,Q thẳng hàng.

Do BM là phân giác góc B nên \(\widehat{MBC}=\widehat{PMB}\left(=\widehat{EBM}\right)\). Vậy EM // BC. Dễ thấy EF // BC nên E, M, F thẳng hàng.

Tương tự Q, P ,E thẳng hàng. 

Vậy M, N, P, Q, E, F thẳng hàng.