Cho hình vẽ
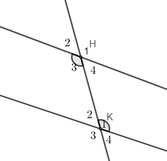
Trong hình trên biết H 3 ⏜ = K 1 ⏜ = 120 o . Trong các khẳng định dưới đây, khẳng định nào sai
A. H 4 ⏜ = K 2 ⏜ = 60 o
B. H 2 ⏜ = K 4 ⏜ = 60 o
C. H 1 ⏜ = K 3 ⏜ = 120 o
D. H 1 ⏜ = K 4 ⏜ = 120 o
Cho mạch điện như hình vẽ
Trong đó UAB=6V, R1=2Ω,R2=R3=4Ω. Số chỉ ampe kế là

1A
0,5A
0,75A
0,25A
a,\(R_{23}=\dfrac{R_2R_3}{R_2+R_3}=\dfrac{4\cdot4}{4+4}=2\left(\Omega\right)\)
\(R_{TĐ}=R_1+R_{23}=2+2=4\left(\Omega\right)\)
\(I_1=I_{23}=I=\dfrac{U_{AB}}{R_{TĐ}}=\dfrac{6}{4}=1,5\left(A\right)\)
\(U_2=U_3=U_{23}=I_{23}R_{23}=1,5\cdot2=3\left(V\right)\)
\(I_A=I_3=\dfrac{U_3}{R_3}=\dfrac{3}{4}=0,75\left(A\right)\)
R1 nt(R2//R3)
\(\Rightarrow I1=\dfrac{U}{R1+\dfrac{R2R3}{R2+R3}}=1,5A=I23\)
\(\Rightarrow U23=U3=I23R23=3V\Rightarrow Ia=I3=\dfrac{U3}{R3}=\dfrac{3}{4}A=0,75A\)
Cho hình bình hành ABCD. Trên BC lấy điểm H, trên BD lấy điểm K sao cho: vecto BH=1/2vecto BC , vecto BK=1/6 vecto BD. C/m 3 điểm A,K,H thẳng hàng
Kham khảo
Câu hỏi của Khanh Quynh - Toán lớp 10 | Học trực tuyến
vào thống kê của mk , nhấn vào chữ màu xanh trog câu tl này sẽ ra
Hc tốt
toi la hai den nha toi toi chi cho
Cho hình Vuông. TRÊN CẠNH AB,BC,CD,DA LẦN LƯỢT LẤY 4 ĐIỂM M, N, P, Q SAO CHO AM = 1/3 AB,BN=1/3 BC, CP=1/3 CD, DQ= 1/3 DA. AN CẮT BP VÀ DM TẠI G VÀ K, CQ CẮT BP VÀ DM TẠI H VÀ I. TÍNH S HÌNH GHIK BIẾT S HÌNH VUÔNG ABCD BẰNG 900 CM VUÔNG
GHI LỜI GIẢI NHÉ
cho hình vuông ABCD. Trên cạnh AB lấy E sao cho BE =1/3AB. Đg thẳng DE cắt BC kéo dài tại K, gọi H là hình chiếu của C trên DE
a) tính S\(_{CDK}\) biết AB =6 cm
b) c/m: CH.KD=CD\(^2\)+ CB.KB
a: AE=6*2/3=4cm
DE=căn 6^2+4^2=2*căn 13(cm)
Xét ΔEAD vuông tạiA và ΔEBK vuông tại B có
góc AED=góc BEK
=>ΔEAD đồng dạng với ΔEBK
=>S EAD/S EBK=(EA/EB)^2=4
=>S EBK=1/2*AE*AD/4=1/2*4*6/4=3(cm2)
Xét ΔKDC có EB//DC
nên ΔKBE đồng dạng với ΔKCD
=>S KBE/S KCD=(EB/DC)^2=1/9
=>S KCD=27cm2
b: CH*KD=CD^2+CB*KB
=>CD*CK-CB^2=CB*KB
=>CB(CK-CB)=CB*KB(đúng)
=>ĐPCM
Cho hình vuông ABCD. Trên các cạnh AB; BC; CD; DA lần lượt lấy 4 điểm M; N; P; Q sao cho AM=1/3 AB; BN=1/3 BC; CP=1/3 CD và DQ=1/3 DA. Nối AN cắt BP và DM tại G và K. Nối CQ cắt BP và DM tại H và I. Tính diện tích GKHI biết diện tích hình vuông ABCD bằng 900 cm2
Cho hình vuông ABCD. Trên các cạnh AB; BC; CD; DA lần lượt lấy 4 điểm M; N; P; Q sao cho AM = 1/3 AB; BN = 1/3 BC; CP = 1/3 CD và DQ = 1/3 DA. Nối AN cắt BP và DM tại G và K. Nối CQ cắt BP và DM tại H và I. Tính diện tích tứ giác GKHI biết diện tích hình vuông ABCD bằng 900cm2.
Tại sao tài khoản này " Phạm Quang Long " được nhiều bạn tích mà sao không được cộng điểm hỏi đáp ???????????
Mong sớm nhận được hồi âm của ONLINE MATH
Xin chân thành cảm ơn!!!!!!!!
Cố gắng gửi câu trả lời kèm theo lời giải nhé!
Cho hình vuông ABCD. Trên cạnh AB; BC;CD;DA lần lượt lấy 4 điểm M;N;P;Q sao cho AM= 1/3 AB, BN=1/3 BC; CP=1/3 CD và DQ=1/3 DA. AN cắt BP và DM tại G và K; CQ cắt BP và DM tại H và I. Tính diện tích tứ giác GHIK biết diện tích hình vuông là 900 cm2
Cho tam gíac ABC vuông tại A, M là trung điểm của BC, H là hình chiếu của M trên AC, K là hình chiếu của H trên BC. Tính diện tích tam giác ABC biết MH=15mm, HK=12mm
Lời giải:
Xét tam giác ADH và AOH có:
\(\widehat{DAH}=\widehat{OAH}\) (gt)
\(\widehat{AHD}=\widehat{AHO}=90^0\)
AH chung
\(\Rightarrow \triangle ADH=\triangle AOH(g.c.g)\) (1)
\(\Rightarrow AD=AO\Rightarrow \frac{AD}{AO}=1\)
Xét tam giác ADH và AOK có:
\(\widehat{AHD}=\widehat{AKO}=90^0\)
\(\widehat{DAH}=\widehat{OAB}=\widehat{OAK}\) (gt)
\(\Rightarrow \triangle ADH\sim \triangle AOK(g.g)\Rightarrow \frac{AH}{AK}=\frac{DH}{OK}=\frac{AD}{AO}=1\Rightarrow AH=AK;DH=OK\)
Vì AO là phân giác của \(\widehat{HAB}\) nên theo tính chất đường phân giác thì:
\(\frac{AH}{AB}=\frac{OH}{OB}\)
Trong đó \(OH=DH\) (do (1)) nên \(OH=\frac{1}{2}OD\). Mà \(OD=OB\) theo tính chất hình bình hành
\(\Rightarrow \frac{AH}{AB}=\frac{OH}{OB}=\frac{1}{2}\)
Mà \(AH=AK\Rightarrow AK=\frac{1}{2}AB\Rightarrow AK=KB\)
Tam giác AOB có OK vừa là đường cao vừa là đường trung tuyến nên tam giác AOB cân tại O. Do đó OA=OB hay AC=BD nên ABCD là hình chữ nhật (đpcm).
Cho hình vuông ABCD. Lấy M ∈BC sao cho BM = \(\dfrac{1}{3}\) BC, lấy N∈tia đối tia CD sao cho CN = \(\dfrac{1}{2}\) BC. Cạnh AM cắt BN tại I và cạnh CI cắt AB tại K. H là hình chiếu của M trên AC. Gọi E là giao điểm của AI và DC.
Chứng minh: K, M, H thẳng hàng