Một con lắc lò xo treo thẳng đứng dao động điều hòa theo phương thẳng đứng, chu kì và biên độ của con lắc lần lượt là 0,4s và 8cm, lấy g = π 2 = 10 m / s 2 . Thời gian lò xo nén trong một chu kì là
A. 2 15 s
B. 4 15 s
C. 7 15 s
D. 11 15 s
Một con lắc lò xo treo thẳng đứng. Kích thích cho con lắc dao động điều hòa theo phương thẳng đứng. Chu kì và biên độ dao động của con lắc lần lượt là 0,4s và 8cm. Chọn trục x’x thẳng đứng, chiều dương hướng xuống, gốc tọa độ tại vị trí cân bằng, gốc thời gian t = 0 khi quả nặng của con lắc qua vị trí cân bằng theo chiều dương. Lấy gia tốc rơi tự do g = 10(m/s2) và π 2 = 10 . Thời gian ngắn nhất kể từ khi t = 0 đến khi lực đàn hồi của lò xo có độ lớn cực tiểu là
A. 7/30s
B. 4/15s
C. 3/10s
D. 1/30s
Đáp án A
Ta có:
![]()
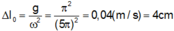
Vì ![]() nên
nên ![]() khi
khi 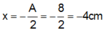 ứng với góc quay trên đường tròn là
ứng với góc quay trên đường tròn là
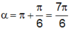
Thời gian cần tính là ![]()
Một con lắc lò xo dao động điều hòa theo phương thẳng đứng với chu kì 0,4s và biên độ 8cm. Lấy g = 10 m/s2 và . Khoảng thời gian ngắn nhất giữa hai lần công suất tức thời của lực đàn hồi bằng 0 là
A.1/30s
B. 2/15s
C. 1/15s
D. 4/15s
Đáp án C
Phương pháp: Sử dụng đường tròn lượng giác
Cách giải:
Công suất tức thời của lực đàn hồi:
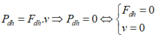
Ta có Fđh = k.∆l nên để Fđh = 0 thì vật phải ở vị trí lò xo không bị biến dạng tức là lúc đó vật ở vị trí x = -∆l
Mặt khác v = 0 khi vật ở vị trí biên.
Bài toán trở thành tìm thời gian ngắn nhất vật đi giữa vị trí biên và vị trí:
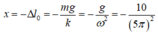

Biểu diễn trên đường tròn lượng giác:
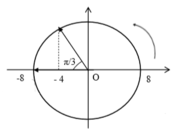
Từ đường tròn lượng giác ta có:
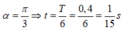
Một con lắc lò xo được treo trên trần một thang máy.Khi con lắc đứng yên thì con lắc được kích thích dao động điều hòa theo phương thẳng đứng với chu lỳ 0,4s, biên đọ 5cm.Vừa lúc quả cầu của con lắc đang đi qua vị trí lò xo không biến dạng theo chiều từ trên xuống thì thang máy chuyển động nhanh dần đều với gia tốc có độ lớn 5m/s2.Lấy g=π=10m/s2.Sau đó con lắc dao động với biên độ bao nhiêu?
Độ biến dạng của lò xo tại vị trí cân bằng: $x=\Delta l=\dfrac{mg}{k}=\dfrac{T^2 g}{4\pi ^2} = 4cm.$
Xét chuyển động của con lắc với thang máy: Chọn chiều dương hướng lên. Thang máy chuyển động nhanh dần đều ở vị trí $x=\Delta l.$
Khi thang máy chuyển động, vị trí cân bằng bị dịch xuống dưới một đoạn bằng: $y=\Delta l=\dfrac{m\left(g+a\right)}{k}-\dfrac{mg}{k}.$
Nên li độ lúc sau là: $x+y.$
Ta có: $A^2=x^2+\left(\dfrac{v}{\omega }\right)^2.$
$A^2=\left(x+y\right)^2+\left(\dfrac{v}{\omega }\right)^2.$
Từ đó ta có: $A^2=A^2+y^2+2xy.$
Tính ra: $A=3 \sqrt{5}.$
một con lắc lò xo treo thẳng đứng. kích thích cho con lắc dao động điều hòa theo phương thẳng đứng . khi đó năng lượng dao động là 0.05 J, độ lớn lớn nhất và nhỏ nhất của lực đàn hồi của lò xo là 6N và 2N. tìm chu kì và biên độ dao động . lây g= 10m/s2
Fmax=k(Δl+A)=6 (1)
Fmin=k(Δl-A)=4 (2)
W=1/2kA^2=0,05 (3)
giải hệ 3 phương trình 3 ẩn được
Δl=5A thay vào(1) rồi lấy (3) chia (1) được A=0,1(m)=10cm
Một con lắc lò xo treo thẳng đứng. Kích thích cho con lắc dao động điều hòa theo phương thẳng đứng. Chu kì và biên độ dao động của con lắc lần lượt là 0,4 s và 8 cm. Chọn trục x ' x thẳng đứng chiều dương hướng xuống, gốc tọa độ tại vị trí cân bằng, gốc thời gian t = 0 khi vật qua vị trí cân bằng theo chiều dương. Lấy gia tốc rơi tự do g = 10 m / s 2 và π 2 = 10. Tốc độ trung bình của vật đi từ khi t = 0 đến khi lực đàn hồi của lò xo có độ lớn cực tiểu lần đầu là
A. 85,7 cm/s
B. 75,8 cm/s
C. 58,7 cm/s
D. 78,5 cm/s
Chọn đáp án A
Δ l = m g k = T 2 4 π 2 g = 0 , 04 m = 4 c m T h ờ i g i a n t ừ x = 0 → x = + A → x = 0 → x = − A 2 T 4 + T 4 + T 12 = 7 T 12 = 7 30 s là:
Tốc độ trung bình:
v = s t = A + A + 0 , 5 A t = 85 , 7 c m / s
Một con lắc lò xo treo thẳng đứng. Kích thích cho con lắc dao động điều hòa theo phương thẳng đứng. Chu kì và biên độ dao động của con lắc lần lượt là 0,4 s và 8 cm. Chọn trục x'x thẳng đứng chiều dương hướng xuống, gốc tọa độ tại vị trí cân bằng, gốc thời gian t = 0 khi vật qua vị trí cân bằng theo chiều dương. Lấy gia tốc rơi tự do g = 10 m/s 2 và π 2 = 10 . Tốc độ trung bình của vật đi từ khi t = 0 đến khi lực đàn hồi của lò xo có độ lớn cực tiểu lần đầu là
A. 85 , 7 cm/s
B. 75,8 cm/s
C. 58 , 7 cm/s
D. 78 , 5 cm/s
Đáp án A
Δ l = m g k = T 2 4 π 2 g = 0 , 04 m = 4 c m
Thời gian từ x = 0 → x = + A → x = 0 → x = − A 2 là: T 4 + T 4 + T 12 = 7 T 12 = 7 30 s
Tốc độ trung bình: v = s t = A + A + 0 , 5 A t = 85 , 7 cm/s
Một con lắc lò xo treo thẳng đứng. Kích thích cho con lắc dao động điều hòa theo phương thẳng đứng. Chu kì và biên độ dao động của con lắc lần lượt là 0,4 s và 8 cm. Chọn trục xx thẳng đứng chiều dương hướng xuống, gốc tọa độ tại vị trí cân bằng, gốc thời gian t = 0 khi vật qua vị trí cân bằng theo chiều dương. Lấy gia tốc rơi tự do g = 10 m / s 2 và π 2 = 10 . Tốc độ trung bình của vật đi từ khi t = 0 đến khi lực đàn hồi của lò xo có độ lớn cực tiểu lần đầu là
A. 85,7 cm/s
B. 75,8 cm/s
C. 58,7 cm/s
D. 78,5 cm/s
Một con lắc lò xo dao động điều hòa theo phương thẳng đứng với biên độ 8 cm. Trong một chu kì, tỉ số thời gian dãn và nén của lò xo là 2. Tình tần số dao động của con lắc. Lấy g = π 2 m / s 2
A. 2,5 Hz.
B. 1 Hz.
C. 2 Hz.
D. 1,25 Hz.
Chọn A.
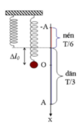
Lò xo dãn khi -A ≤ x ≤ ∆ l 0 và nén khi ∆ l 0 ≤ x ≤ A Vì thời
gian dãn gấp đôi thời gian nén nên ∆ l 0 = A / 2 = 0 , 04 m
Tần số:
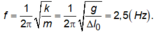
Một con lắc lò xo treo thẳng đứng. Kích thích cho con lắc dao động điều hòa theo phương thẳng đứng. Chu kì và biên độ dao động của con lắc lần lượt là 0,4 s và 8 cm. Chọn trục x'x thẳng đứng chiều dương hướng xuống, gốc tọa độ tại vị trí cân bằng, gốc thời gian t = 0 khi vật qua vị trí cân bằng theo chiều dương. Lấy gia tốc rơi tự do g = 10 m / s 2 và π 2 = 10 . Tốc độ trung bình của vật đi từ khi t = 0 đến khi lực đàn hồi của lò xo có độ lớn cực tiểu lần đầu là
A. 85,7 cm/s
B. 75,8 cm/s
C. 58,7 cm/s
D. 78,5 cm/s