Không vẽ hình, hãy cho biết hệ phương trình sau có bao nhiêu nghiệm.
x − 2 y + 10 = 0 − 3 x + 6 y − 30 = 0
A. 1
B. Vô số
C. 0
D. 2
Không cần vẽ hình, cho biết mỗi hệ phương trình sau có bao nhiêu nghiệm?
y = 2 x + 10 y = x + 100
A. 1
B. Vô số
C. 0
D. 2
Đáp án A
+ Tập nghiệm của phương trình y = 2x + 10 được biểu diễn bởi đường thẳng d 1 :y = 2x + 10.
+ Tập nghiệm của phương trình y = x + 100 được biểu diễn bởi đường thẳng d 2 : y = x + 100.
Lại có: hệ số góc của hai đường thẳng d 1 ; d 2 khác nhau (2 ≠ 1) nên hai đường thẳng này cắt nhau.
Suy ra, hệ phương trình đã cho có nghiệm duy nhất.
Không giải các hẹ phương trình sau, hãy cho biết mỗi hệ phương trình có bao nhiêu nghiệm? Vì sao?
![]()
![]()
![]()
Không cần vẽ hình, hãy cho biết số nghiệm của mỗi hệ phương trình sau đây và giải thích vì sao:
y = - 1 2 y = - 1 2 x + 1
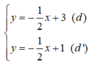
Xét (d): 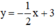 có a =
có a = 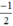 ; b = 3
; b = 3
(d’): 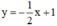 có a’ =
có a’ = 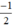 ; b’ = 1.
; b’ = 1.
Có a = a’; b ≠ b’ ⇒ (d) // (d’)
⇒ Hệ phương trình 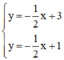 vô nghiệm
vô nghiệm
Không cần vẽ hình, hãy cho biết số nghiệm của mỗi hệ phương trình sau đây và giải thích vì sao:
y = 3 - 2 x y = 3 x - 1
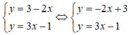
Xét (d): y = -2x + 3 có a = -2; b = 3
(d’) : y = 3x – 1 có a’ = 3 ; b’ = -1.
Có a ≠ a’ ⇒ (d) cắt (d’)
⇒ Hệ 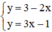 có nghiệm duy nhất.
có nghiệm duy nhất.
Không cần vẽ hình, hãy cho biết số nghiệm của mỗi hệ phương trình sau đây và giải thích vì sao:
3 x - y = 3 x - 1 3 y = 1
Ta có:
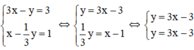
Ta có: a = a’=3; b = b’ = -3
Nhận thấy hai đường thẳng trên trùng nhau
⇒ Hệ phương trình có vô số nghiệm.
Kiến thức áp dụng
Không vẽ hình, hỏi hệ phương trình sau có bao nhiêu nghiệm:
- 2 x + 5 y = 10 16 x - 40 y = 20
A. Vô số nghiệm
B. 0
C.1
D. 2
Đáp án B
Ta có:
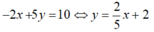
Nên tập nghiệm của phương trình – 2x + 5y = 10 được biểu diễn bởi đường thẳng ( d 1 ):
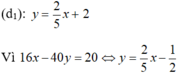
Nên tập nghiệm của phương trình 16x – 40y = 20 được biểu diễn bởi đường thẳng ( d 2 ):
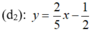
Hai đường thẳng d 1 ; d 2 có cùng hệ số góc và có tung độ góc khác nhau nên d 1 // d 2 .
Suy ra, hệ phương trình đã cho vô nghiệm.
Cho các hệ phương trình sau: x = 2 2 x - y = 3
Trước hết, hãy đoán nhận số nghiệm của mỗi hệ phương trình trên (giải thích rõ lí do). Sau đó, tìm tập nghiệm của các hệ đã cho bằng cách vẽ hình.
x = 2 2 x - y = 3
Đường thẳng (d): x = 2 song song với trục tung.
Đường thẳng (d’): 2x – y = 3 không song song với trục tung
⇒ (d) cắt (d’)
⇒ Hệ có nghiệm duy nhất.
Vẽ (d): x = 2 là đường thẳng đi qua (2 ; 0) và song song với trục tung.
Vẽ (d’): 2x - y = 3
- Cho x = 0 ⇒ y = -3 được điểm (0; -3).
- Cho y = 0 ⇒ x = 1,5 được điểm (1,5 ; 0).
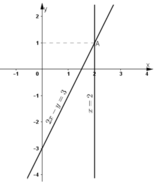
Ta thấy hai đường thẳng (d) và (d’) cắt nhau tại A(2; 1).
Vậy hệ phương trình có nghiệm (2; 1).
Cho các hệ phương trình sau:
a ) x = 2 2 x − y = 3 b ) x + 3 y = 2 2 y = 4
Trước hết, hãy đoán nhận số nghiệm của mỗi hệ phương trình trên (giải thích rõ lí do). Sau đó, tìm tập nghiệm của các hệ đã cho bằng cách vẽ hình.
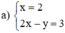
Đường thẳng (d): x = 2 song song với trục tung.
Đường thẳng (d’): 2x – y = 3 không song song với trục tung
⇒ (d) cắt (d’)
⇒ Hệ có nghiệm duy nhất.
Vẽ (d): x = 2 là đường thẳng đi qua (2 ; 0) và song song với trục tung.
Vẽ (d’): 2x - y = 3
- Cho x = 0 ⇒ y = -3 được điểm (0; -3).
- Cho y = 0 ⇒ x = 1,5 được điểm (1,5 ; 0).
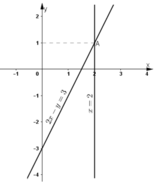
Ta thấy hai đường thẳng (d) và (d’) cắt nhau tại A(2; 1).
Vậy hệ phương trình có nghiệm (2; 1).
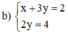
Đường thẳng (d): x + 3y = 2 không song song với trục hoành
Đường thẳng (d’): 2y = 4 hay y = 2 song song với trục hoành
⇒ (d) cắt (d’)
⇒ Hệ phương trình có nghiệm duy nhất.
Vẽ (d1): x + 3y = 2
- Cho y = 0 ⇒ x = 2 được điểm (2; 0).
- Cho x = 0 ⇒ y = 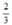 được điểm (0;
được điểm (0; 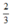 ).
).
Vẽ (d2): y = 2 là đường thẳng đi qua (0; 2) và song song với trục hoành.
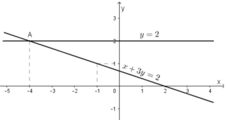
Ta thấy hai đường thẳng (d) và (d’) cắt nhau tại A(-4; 2).
Vậy hệ phương trình có nghiệm (-4; 2).
Không cần vẽ hình, hãy cho biết số nghiệm của mỗi hệ phương trình sau đây và giải thích vì sao:
2 y = - 3 x 3 y = 2 x
Ta có: 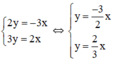
Xét (d): y = 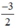 x có a =
x có a = 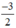 ; b = 0
; b = 0
(d’) : y = 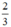 x có a’ =
x có a’ = 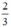 ; b’ = 0
; b’ = 0
Ta có: a ≠ a’ ⇒ (d) cắt (d’)
⇒ Hệ 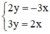 có nghiệm duy nhất.
có nghiệm duy nhất.