Cho tứ diện đều cạnh a, điểm I nằm trong tứ diện. Tính tổng khoảng cách từ I đến tất cả các mặt của tứ diện.
A. a 6 3
B. a 2
C. a 3 3
D. a 34 3
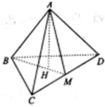
Cho tứ diện đều ABCD có cạnh bằng a. M là một điểm bất kì bên trong tứ diện. Tổng khoảng cách từ M đến các mặt của khối tứ diện là
A. Một đại lượng phụ thuộc vị trí của M
B. a 2 3
C. a 2
D. a 3
Chọn B.
Gọi x, y, z, t lần lượt là khoảng cách từ M đến các mặt phẳng (BCD), (CDA), (DAB), (ABC). Ta có

Cộng lại ta thu được (chú ý rằng)
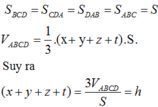
với h là độ dài đường cao của tứ diện đều ABCD. Ta có
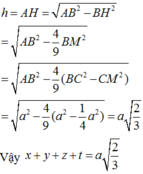
Cho tứ diện đều ABCD có cạnh bằng a. Gọi M là một điểm thuộc miền trong của khối tứ diện tương ứng. Giá trị lớn nhất của tích các khoảng cách từ điểm M đến bốn mặt phẳng của tứ diện đã cho là
A. a 4 521
B. a 4 576
C. a 4 6 81
D. a 4 6 324
Chọn đáp án B
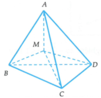
Gọi r1, r2, r3, r4 lần lượt là khoảng cách từ điểm M đến các mặt phẳng (BCD), (ACD), (ABD), (ABC)
Gọi S là diện tích một mặt của tứ diện đều thì
Thể tích tứ diện đều ABCD là V A B C D = a 3 2 12
Ta có V A B C D = V M . B C D + V M . A C D + V M . A B D + V M . A B C
![]()
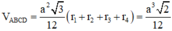
Áp dụng bất đẳng thức Cauchy cho các số dương ta có:
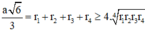
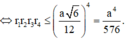
Dấu “=” xảy ra khi và chỉ khi
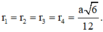
Cho tứ diện đều ABCD. Biết khoảng cách từ điểm A đến mặt phẳng (BCD) bằng 6. Tính thể tích của tứ diện ABCD
A. V = 27 3
B. C. V = 27 3 2 D. V = 9 3 2
C. V = 27 3 2
D. V = 9 3 2
Cho tứ diện đều ABCD. Biết khoảng cách từ điểm A đến mặt phẳng (BCD) bằng 6. Tính thể tích của tứ diện ABCD
A. V = 27 3
B. V = 5 3
C. V = 27 3 2
D. V = 9 3 2
Đáp án A
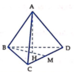
Gọi H là hình chiếu của điểm A trên mặt phẳng(BCD). Do ABCD là tứ diện đều nên tâm H là tâm đường trong ngoại tiếp Δ B C D .
Đặt cạnh của tứ diện là a. Gọi M là trung điểm của CD.
Do Δ B C D đều nên
B M = a 3 2 ⇒ B H = 2 3 B M = 2 3 . a 3 2 = a 3 3
Ta có Δ A B H vuông tại H nên
A H = A B 2 − B H 2 = a 2 − a 3 3 2 = a 6 3
Từ giả thiết ta có
A H = a 6 3 = 6 ⇔ a = 3 6 ⇒ S Δ B C D = a 2 3 4 = 27 3 2
(đvdt).
Vậy thể tích của tứ diện ABCD là
A H = a 6 3 = 6 ⇔ a = 3 6 ⇒ S Δ B C D = a 2 3 4 = 27 3 2
(đvtt).
Cho tứ diện đều ABCD. Biết khoảng cách từ điểm A đến mặt phẳng (BCD) bằng 6. Tính thể tích của tứ diện ABCD
A. V = 27 3
B. V = 5 3
C. V = 27 3 2
D. V = 9 3 2
Đáp án A
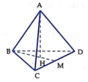
Gọi H là hình chiếu của điểm A trên mặt phẳng (BCD). Do ABCD là tứ diện đều nên tâm H là tâm đường trong ngoại tiếp ∆ BCD.
Đặt cạnh của tứ diện là a. Gọi M là trung điểm của CD.
Do ∆ BCD đều nên
![]()
![]()
Ta có ∆ ABH vuông tại H nên
![]()
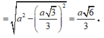
Từ giả thiết ta có
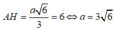
![]()
Vậy thể tích của tứ diện ABCD là
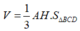
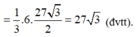
Tứ diện đều ABCD có khoảng cách từ điểm A đến mặt phẳng (BCD) = a. Cạnh của tứ diện có độ dài bằng?
A. a 6 3
B. a 6 2
C. a 2 3
D. a 2 2
Tứ diện đều ABCD có khoảng cách từ điểm A đến mặt phẳng bằng a. Cạnh của tứ diện có độ dài bằng
A. a 6 3
B. a 6 2
C. a 2 3
D. a 2 2
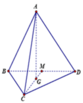
Tứ diện đều ABCD có khoảng cách từ điểm A đến mặt phẳng (BCD) bằng a. Cạnh của tứ diện có độ dài bằng?
A. a 6 3
B. a 6 2
C. a 2 3
D. a 2 2
Đáp án A
Gọi G là trọng tâm tam giác đều ABC suy ra G A ⊥ ( B C D )
Gọi M là trung điểm BD.
Đặt A C = x ⇒ G C = 2 3 C M = x 3 3
lại có A C 2 - G C 2 = A G 2
![]()
⇒ x = a 6 2
Tính tổng diện tích tất cả các mặt của tứ diện đều cạnh a
A. 4 a 2 3
B. a 2 3 2
C. a 2 3 4
D. a 2 3