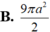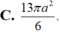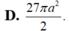Cho hình trụ có thiết diện qua trục là hình vuông cạnh bằng 4 cm. Diện tích toàn phần S t p của trụ là
A. S t p = 12 π c m 2 .
B. S t p = 24 π c m 2 .
C. S t p = 16 π c m 2 .
D. S t p = 32 π c m 2 .
Những câu hỏi liên quan
Xét hình trụ T có thiết diện qua trục của hình trụ là hình vuông có cạnh bằng a. Tính diện tích toàn phần S của hình trụ A.
S
4
πa
2
B.
S
3
πa
2
2
C.
S
πa
2
2
D.
πa
2
Đọc tiếp
Xét hình trụ T có thiết diện qua trục của hình trụ là hình vuông có cạnh bằng a. Tính diện tích toàn phần S của hình trụ
A. S = 4 πa 2
B. S = 3 πa 2 2
C. S = πa 2 2
D. πa 2
Cho hình trụ (T) có thiết diện qua trục là hình vuông có cạnh bằng a. Tính diện tích toàn phần
S
t
p
của hình trụ. A.
S
t
p
3
π
a
2
2
B.
S
t
p...
Đọc tiếp
Cho hình trụ (T) có thiết diện qua trục là hình vuông có cạnh bằng a. Tính diện tích toàn phần S t p của hình trụ.
A. S t p = 3 π a 2 2
B. S t p = π a 2
C. S t p = 4 π a 2
D. S t p = π a 2 2
Chọn A
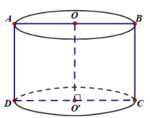
* Theo hình vẽ, do ABCD là hình vuông cạnh a nên ta có:
Đúng 0
Bình luận (0)
Diện tích toàn phần của hình trụ có thiết diện qua trục là hình vuông cạnh a bằng A.
2
πa
2
B.
3
πa
2
2
C.
πa
2
D.
πa
2
2
Đọc tiếp
Diện tích toàn phần của hình trụ có thiết diện qua trục là hình vuông cạnh a bằng
A. 2 πa 2
B. 3 πa 2 2
C. πa 2
D. πa 2 2
Đáp án B
Phương pháp:
Diện tích xung quanh của hình trụ: Sxq = 2πRh
Diện tích toàn phần của hình trụ: Stp = Sxq + S2đáy = 2πRh + 2πR2
Cách giải:
Thiết diện qua trục là hình vuông cạnh a nên hình trụ đã cho có chiều cao h = a, bán kính đáy R = a 2
Diện tích toàn phần của hình trụ là:
Đúng 0
Bình luận (0)
Cắt một hình trụ bởi một mặt phẳng qua trục của nó, ta được thiết diện là một hình vuông có cạnh bằng 3.a Tính diện tích toàn phần của hình trụ đã cho
Đọc tiếp
Cắt một hình trụ bởi một mặt phẳng qua trục của nó, ta được thiết diện là một hình vuông có cạnh bằng 3.a Tính diện tích toàn phần của hình trụ đã cho
Cắt một hình trụ bởi một mặt phẳng qua trục của nó, ta được thiết diện là một hình vuông có cạnh bằng 3.a Tính diện tích toàn phần của hình trụ đã cho A. B. C. D.
Đọc tiếp
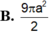
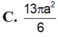
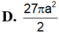
Cắt một hình trụ bởi một mặt phẳng qua trục của nó, ta được thiết diện là một hình vuông có cạnh bằng 3.a Tính diện tích toàn phần của hình trụ đã cho
A.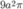 
B.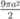 
C.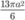 
D.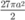 
Thiết diện qua trục của một hình trụ là một hình vuông cạnh a, diện tích toàn phần của hình trụ
Cắt một hình trụ bởi một mặt phẳng qua trục của nó, ta được thiết diện là một hình vuông có cạnh bằng 3a. Tính diện tích toàn phần của hình trụ đã cho A.
9
a
2
π
B.
9
πa
2
2
C.
13
πa...
Đọc tiếp
Cắt một hình trụ bởi một mặt phẳng qua trục của nó, ta được thiết diện là một hình vuông có cạnh bằng 3a. Tính diện tích toàn phần của hình trụ đã cho
A. 9 a 2 π
B. 9 πa 2 2
C. 13 πa 2 6
D. 27 πa 2 2
Cắt một hình trụ bởi một mặt phẳng qua trục của nó, ta được thiết diện là một hình vuông có cạnh bằng 3a. Tính diện tích toàn phần của hình trụ đã cho. A.
9
a
2
π
.
B.
9
π
a
2
2
.
C.
1...
Đọc tiếp
Cắt một hình trụ bởi một mặt phẳng qua trục của nó, ta được thiết diện là một hình vuông có cạnh bằng 3a. Tính diện tích toàn phần của hình trụ đã cho.
A. 9 a 2 π .
B. 9 π a 2 2 .
C. 13 π a 2 6 .
D. 27 π a 2 2 .
Cắt một hình trụ bởi một mặt phẳng qua trục của nó, ta được thiết diện là một hình vuông có cạnh bằng 3a. Tính diện tích toàn phần của hình trụ đã cho.
Đọc tiếp
Cắt một hình trụ bởi một mặt phẳng qua trục của nó, ta được thiết diện là một hình vuông có cạnh bằng 3a. Tính diện tích toàn phần của hình trụ đã cho.
