Để giá trị nhỏ nhất của hàm số y = x + 1 x - m trên khoảng 0 ; + ∞ bằng -3 thì giá trị của tham số m là:
A. m =7
B. m = 19 3 .
C. m = 11 2 .
D. m =5
Để giá trị nhỏ nhất của hàm số y = x + 1 x - m trên khoảng (0;+∞) bằng –3 thì giá trị của tham số m là:
A. m = 11 2
B. m = 19 3
C. m = 5
D. m = 7
Đáp án C.
Phương pháp: Sử dung BĐT Cauchy.
Cách giải: 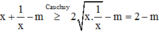
![]()
Để giá trị nhỏ nhất của hàm số y = x + 1 x - m trên khoảng ( 0 ; + ∞ ) bằng -3 thì giá trị của tham số m là:
![]()
![]()
![]()
![]()
cho hàm số y = 2x2 - (m - 1 )x +3, m là tham số
a. tìm khoảng đồng biến, nghịch biến của hàm số
b/ tìm các giái trị của m để hàm số đồng biến trên khoảng 1;+∞
c. tìm m để hàm số nghịch biến trên khoàng -4;8
d. tìm m để giá trị nhỏ nhất của hàm số là 9
Gọi m là giá trị nhỏ nhất của hàm số y = x + 4 x trên khoảng 0 ; + ∞ . Tìm m
![]()
![]()
![]()
![]()
Cho hàm số y = (3 – m)x2a) Tìm điều kiện của m để hàm số trên được xác định.b) Xác định m để hàm số đồng biến với mọi x < 0.c) Xác định m để y = 0 là giá trị nhỏ nhất của hàm số tại x = 0.
a, ĐKXĐ để hàm được xác định : \(3-m\ne0\)
\(\Leftrightarrow m\ne3\)
b, - Với x < 0 để hàm số đồng biến thì : \(3-m< 0\)
\(\Leftrightarrow m>3\)
Vậy ...
c, - Để y = 0 là giá trị nhỏ nhất của hàm số tại x = 0
\(\Leftrightarrow a>0\)
\(\Leftrightarrow3-m>0\)
\(\Leftrightarrow m< 3\)
Vậy ...
a) Để hàm số \(y=\left(3-m\right)x^2\) được xác định thì \(3-m\ne0\)
hay \(m\ne3\)
b) Để hàm số \(y=\left(3-m\right)x^2\) đồng biến với mọi x<0 thì \(3-m< 0\)
\(\Leftrightarrow m>3\)
c) Để y=0 là giá trị nhỏ nhất của hàm số tại x=0 thì 3-m>0
hay m<3
Tìm giá trị nhỏ nhất của hàm số y = x + x 4 trên khoảng ( 0 ; + ∞ )
A. m i n 0 ; + ∞ y = 2
B. m i n 0 ; + ∞ y = 4
C. m i n 0 ; + ∞ y = 0
D. m i n 0 ; + ∞ y = 3
Cho hàm số y=f(x) có đạo hàm xác định trên tập R / - 1 và đồ thị hàm số y=f(x) như hình vẽ. Gọi m, M lần lượt là giá trị nhỏ nhất và giá trị nhỏ nhất của hàm số y=f(sin2x) trên 0 ; π 2 . Tính P=m.M
A. P=0
B. P=8
C. P=12
D. P=4
Cho hàm số y = x − m 2 x + 8 với m là tham số thực. Giả sử m 0 là giá trị dương của tham số m để hàm số có giá trị nhỏ nhất trên đoạn 0 ; 3 bằng − 3. Giá trị m 0 thuộc khoảng nào trong các khoảng cho dưới đây?
A. 20 ; 25 .
B. 5 ; 6 .
C. 6 ; 9 .
D. 2 ; 5 .
Cho hàm số y = x - m 2 x + 8 với m là tham số thực. Giả sử m 0 là giá trị dương của tham số m để hàm số có giá trị nhỏ nhất trên đoạn [0;3] bằng -3. Giá trị m 0 thuộc khoảng nào trong các khoảng cho dưới đây?
A. (20;25)
B. (5;6)
C. (6;9)
D. (2;5)
Chọn D
* Tập xác định ![]()
* Ta có 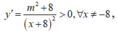
suy ra hàm số đã cho đồng biến trên đoạn [0;3].
Do đó 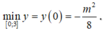
* Theo yêu cầu bài toán ta có: 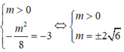
![]()