Cho ba điểm X, Y, Z không thẳng hàng.
Ta nói gì về hai đường thẳng XY và YZ
Những câu hỏi liên quan
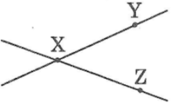
Cho ba điểm X, Y, Z không thẳng hàng. Ta nói gì về hai đường thẳng XY và XZ ?
Xem thêm câu trả lời
câu 10 cho ba điểm X,Y,Z không thẳng hàng, vẽ các đường thẳng XY và XZ.Ta nói gì về hai đường hẳng XY và XZ
hai đường thẳng xy và xz không song song
hai đường thẳng xy và xz chung gốc z
Đúng 0
Bình luận (0)
cho ba điểm X, Y, Z ko thẳng hàng ta nói gì về hai đường thẳng XY và XZ
cho ba điểm x,y,z không thẳng hàng ta nói gì về hai đường thẳng xy va xz
Xem thêm câu trả lời
Cho 3 điểm X,Y,Z ko thẳng hàng. Ta nói gì về hai đường thẳng XY và XZ
XY và XZ là hai đường thẳng phân biệt
Đúng 0
Bình luận (0)
Cho ba điểm A, B, C không thẳng hàng. Ta nói gì về hai đường thẳng AB và AC
A. Trùng nhau
B. Song song
C. Cắt nhau
D. Đáp án khác
Đáp án là C
Vì A, B, C không thẳng hàng nên AB và AC phân biệt
Mà AB và AC có điểm chung duy nhất là A nên hai đường thẳng AB và AC cắt nhau
Đúng 0
Bình luận (0)
a/ Qua hai điểm phân biệt thì kẻ được một đường thẳng.Nếu lấy 10 điểm phân biệt trong đó không có 3 điểm nào thẳng hàng.Ta kẻ được bao nhiêu đường thẳng?b/ Nếu lấy n điểm phân biệt (n thuộc N,n lớn hơn hoặc 2)Trong đó không có ba điểm nào thẳng hàng.Ta kẻ được bao nhiêu đường thẳng đi qua các cặp điểm ?c/ Cho 1001 điểm phân biệt,qua hai điểm ta sẽ vẽ một đoạn thẳng.Có tất că bao nhiêu đoạn thẳng
Đọc tiếp
a/ Qua hai điểm phân biệt thì kẻ được một đường thẳng.Nếu lấy 10 điểm phân biệt trong đó không có 3 điểm nào thẳng hàng.Ta kẻ được bao nhiêu đường thẳng?
b/ Nếu lấy n điểm phân biệt (n thuộc N,n lớn hơn hoặc = 2)Trong đó không có ba điểm nào thẳng hàng.Ta kẻ được bao nhiêu đường thẳng đi qua các cặp điểm ?
c/ Cho 1001 điểm phân biệt,qua hai điểm ta sẽ vẽ một đoạn thẳng.Có tất că bao nhiêu đoạn thẳng
Bài 1: Vẽ đường thẳng a. Lấy A in a, B in a, C in a, D notin a . Kẻ các đường thẳng đi qua các cặp điểm.a) Kẻ được tất cả bao nhiêu đường thẳng ( phân biệt )?b) Viết tên các đường thẳng đó?c) D là giao điểm của những đường thẳng nào?Bài 2: Cho hai điểm A,Ba)Vẽ đường thẳng đi qua điểm A. Có tất cả bao nhiêu đường thẳng?b) Vẽ đường thẳng đi qua A và B. Có tất cả bao nhiêu đường thẳng?Bài 3: Cho ba điểm X,Y,Z không thẳng hàng. Ta nói gì về hai đường thẳng XY và XZ ? Làm được bài nào thì là...
Đọc tiếp
Bài 1: Vẽ đường thẳng a. Lấy A \(\in\) a, B \(\in\) a, C \(\in\) a, D \(\notin\) a . Kẻ các đường thẳng đi qua các cặp điểm.
a) Kẻ được tất cả bao nhiêu đường thẳng ( phân biệt )?
b) Viết tên các đường thẳng đó?
c) D là giao điểm của những đường thẳng nào?
Bài 2: Cho hai điểm A,B
a)Vẽ đường thẳng đi qua điểm A. Có tất cả bao nhiêu đường thẳng?
b) Vẽ đường thẳng đi qua A và B. Có tất cả bao nhiêu đường thẳng?
Bài 3: Cho ba điểm X,Y,Z không thẳng hàng. Ta nói gì về hai đường thẳng XY và XZ ?
Làm được bài nào thì làm nha !
Bài 3:
Hai đường XY và XZ đồng quy tại điểm X
Đúng 0
Bình luận (0)
Trong Hình 6 có ba đoạn thẳng được đánh số (1), (2), (3) và hai điểm A, B
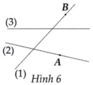
Hãy xác định đường thẳng nào là đường thẳng x, y , z biết
- Đường thẳng x đi qua điểm A;
- Đường thẳng y chứa điểm B;
- Đường thẳng z không đi qua hai điểm A và B
Đường thẳng x là đường thẳng số (2). Đường thẳng y là đường thẳng số (1). Đường thẳng z là đường thẳng số (3)
Đúng 0
Bình luận (0)