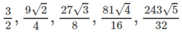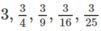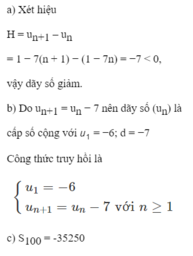Viết năm số hạng đầu và khảo sát tính tăng, giảm của các dãy số ( u n ) biết u n = 3 n - 7

Những câu hỏi liên quan
Viết năm số hạng đầu và khảo sát tính tăng, giảm của các dãy số ( u n ) biết u n = 3 n n 2 n
Viết năm số hạng đầu và khảo sát tính tăng, giảm của các dãy số u n biết u n = 2 n + 1 n 2
Viết năm số hạng đầu và khảo sát tính tăng, giảm của các dãy số ( u n ) biết u n = 10 1 - 2 n
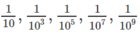
Dự đoán dãy (un) giảm.
Để chứng minh, ta xét tỉ số
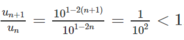 .
.
Vậy dãy số giảm
Đúng 0
Bình luận (0)
Cho dãy số
(
u
n
)
với
u
n
1
-
7
n
a) Khảo sát tính tăng, giảm của dãy số;b) Chứng minh dãy số trên là cấp số cộng. Lập công thức truy hồi của dãy số;c) Tính tổng 100 số hạng đầu của dãy số.
Đọc tiếp
Cho dãy số ( u n ) với u n = 1 - 7 n
a) Khảo sát tính tăng, giảm của dãy số;
b) Chứng minh dãy số trên là cấp số cộng. Lập công thức truy hồi của dãy số;
c) Tính tổng 100 số hạng đầu của dãy số.
Viết năm số hạng đầu và khảo sát tính năng, giảm của các dãy số \(\left(u_n\right)\), biết :
a) \(u_n=10^{1-2n}\)
b) \(u_n=3^n-7\)
c) \(u_n=\dfrac{2n+1}{n^2}\)
d) \(u_n=\dfrac{3^n\sqrt{n}}{2^n}\)
a)
\(u_1=10^{1-2.1}=10^{-1};u_2=10^{1-2.2}=10^{-3}\);
\(u_3=10^{1-2.3}=10^{-5}\); \(u_4=10^{1-2.4}=10^{-7}\);
\(u_5=10^{1-2.5}=10^{-9}\).
Xét \(\dfrac{u_n}{u_{n-1}}=\dfrac{10^{1-2n}}{10^{1-2\left(n-1\right)}}=\dfrac{10^{1-2n}}{10^{3-2n}}=10^{-2}=\dfrac{1}{100}\).
Suy ra: \(u_n=\dfrac{1}{100}u_{n-1}\) và dễ thấy \(\left(u_n\right)>0,\forall n\in N^{\circledast}\) nên \(u_n< u_{n-1},\forall n\ge2\).
Vậy \(\left(u_n\right)\) là dãy số tăng.
Đúng 0
Bình luận (0)
b) \(u_1=3^1-7=-4\); \(u_2=3^2-7=2\); \(u_3=3^3-7=25\);
\(u_4=3^4-7=74\); \(u_5=3^5-7=236\).
\(u_n-u_{n-1}=3^n-7-\left(3^{n-1}-7\right)=3^n-3^{n-1}=2.3^{n-1}\)\(\left(n\ge2\right)\).
Với \(n\ge2\) thì \(2.3^{n-1}>0\) nên \(u_n>u_{n-1}\).
Vậy \(\left(u_n\right)\) là dãy số tăng.
Đúng 0
Bình luận (0)
c)
\(u_1=\dfrac{2.1+1}{1^2}=2;u_2=\dfrac{2.2+1}{2^2}=\dfrac{5}{2}\);
\(u_3=\dfrac{2.3+1}{3^2}=\dfrac{7}{9}\); \(u_4=\dfrac{2.4+1}{4^2}=\dfrac{9}{16}\); \(u_5=\dfrac{2.5+1}{5^2}=\dfrac{11}{25}\);
\(u_n=\dfrac{2n+1}{n^2}=\dfrac{2}{n}+\dfrac{1}{n^2}\);
\(u_{n+1}=\dfrac{2}{n+1}+\dfrac{1}{\left(n+1\right)^2}\);
Vì\(n+1>n\) nên suy ra:
\(\dfrac{2}{n+1}< \dfrac{2}{n}\)
\(\dfrac{1}{\left(n+1\right)^2}< \dfrac{1}{n^2}\)
Cộng từng vế của bất đẳng thức ta có:
\(\dfrac{2}{n+1}+\dfrac{1}{\left(n+1\right)^2}< \dfrac{2}{n}+\dfrac{1}{n^2}\)
\(\Leftrightarrow u_{n+1}< u_n\).
Vậy \(\left(u_n\right)\) là dãy số giảm
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho dãy số (U n) với U n = 2n/ n^2 + 1 , ∀ n ∈ N*
a) Viết 5 số hạng đầu
b) số 9/U¹ là hạng thứ mấy
c) chứng minh dãy số bị giảm và bị chặn
Xem chi tiết
Cho dãy số (U n) với U n = 2n/ n^2 + 1 , ∀ n ∈ N*
a) Viết 5 số hạng đầu
b) số 9/U¹ là hạng thứ mấy
c) chứng minh dãy số bị giảm và bị chặn
Xem chi tiết
Cho dãy số:
\(u:{\mathbb{N}^*} \to \mathbb{R}\)
\(n \mapsto {u_n} = {n^3}\)
a) Hãy cho biết dãy số trên là hữu hạn hay vô hạn.
b) Viết năm số hạng đầu tiên của dãy số đã cho.
a) Vì hàm số \(u\) xác định trên tập hợp các số nguyên dương
\(\mathbb{N}^{\text{∗
}}\) nên nó là một dãy số vô hạn.
b) Ta có:
\(u_1=1^3=1\\ u_2=2^3=8\\ u_3=3^3=27\\ u_4=4^3=64\\ u_5=5^3=125.\)
Đúng 2
Bình luận (0)
a: Dáy số này là vô hạng
b: 1;8;27;64;125
Đúng 0
Bình luận (0)
Cho dãy số \(\left(u_n\right)\) với \(u_n=1-7n\)
a) Khảo sát tính tăng, giảm của dãy số
b) Chứng minh dãy số trên là cấp số cộng. Lập công thức truy hồi của dãy số
c) Tính tổng 100 số hạng đầu của dãy số