Xét tính đồng biến, nghịch biến và tính giá trị lớn nhất, giá trị nhỏ nhất của hàm số:
y = x 2 trên đoạn [-3; 0];
Xét tính đồng biến, nghịch biến và tính giá trị lớn nhất, giá trị nhỏ nhất của hàm số:
y = (x + 1)/(x - 1) trên đoạn [3; 5].
y ' = - 2 x - 1 2 < 0 trên đoạn [3; 5]. Vậy hàm số nghịch biến trên đoạn [3; 5].
Khi đó trên đoạn [-3,5]: hàm số đạt giá trị lớn nhất tại x = 3 và giá trị lớn nhất bằng 2, hàm số đạt giá trị nhỏ nhất tại x = 5 và giá trị nhỏ nhất = 1.5.
Xét tính đồng biến, nghịch biến và tính giá trị lớn nhất, giá trị nhỏ nhất của hàm số:
a) y = x2 trên đoạn [-3; 0];
b) y = trên đoạn [3; 5].
Cho hàm số y=f(x) = 4x^2+ 6x-5 a) Lập bảng biến thiên và vẽ đồ thị hàm số y= f(×). b) Từ bảng biến thiên, xác định khoảng đồng biến và nghịch biến và giá trị nhỏ nhất của hàm số trên c) Từ bảng biến thiên tìm giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số trên đoạn [-1;2]
a: Tọa độ đỉnh là:
\(\left\{{}\begin{matrix}x=\dfrac{-6}{2\cdot4}=\dfrac{-6}{8}=\dfrac{-3}{4}\\y=-\dfrac{6^2-4\cdot4\cdot\left(-5\right)}{4\cdot4}=-\dfrac{29}{4}\end{matrix}\right.\)
Bảng biến thiên là:
| x | -\(\infty\) -3/4 +\(\infty\) |
| y | -\(\infty\) -29/4 +\(\infty\) |

b: Hàm số đồng biến khi x>-3/4; nghịch biến khi x<-3/4
GTNN của hàm số là y=-29/4 khi x=-3/4
Cho hàm số y=f(x)= -3x^2+10x-4 a) Lập bảng biến thiên và vẽ đồ thị hàm số y= f(×) b) Từ bảng biến thiên, xác định khoảng đồng biến và nghịch biến và giá trị nhỏ nhất của hàm số trên c) Từ bảng biến thiên tìm giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số trên đoạn [-1;2]
a: Tọa độ đỉnh là:
\(\left\{{}\begin{matrix}x=\dfrac{-10}{2\cdot\left(-3\right)}=\dfrac{10}{6}=\dfrac{5}{3}\\y=-\dfrac{10^2-4\cdot\left(-3\right)\cdot\left(-4\right)}{4\cdot\left(-3\right)}=\dfrac{13}{3}\end{matrix}\right.\)
Bảng biến thiên:
| x | -\(\infty\) 5/3 +\(\infty\) |
| y | +\(\infty\) 13/3 -\(\infty\) |

b: Hàm số đồng biến khi x<5/3; nghịch biến khi x>5/3
Giá trị nhỏ nhất là y=13/3 khi x=5/3
Hãy vẽ đồ thị của các hàm số y = 2x2, y = -2x2. Dựa vào đồ thị để trả lời các câu hỏi sau:
Nếu a > 0 thì hàm số y = ax2 đồng biến khi nào? Nghịch biến khi nào?
Với giá trị nào của x thì hàm số đạt giá trị nhỏ nhất? Có giá trị nào của x để hàm số đạt giá trị lớn nhất không?
Nếu a < 0 thì hàm số đồng biến khi nào? Nghịch biến khi nào? Với giá trị nào của x thì hàm số đạt giá trị lớn nhất? Có giá trị nào của x để hàm số đạt giá trị nhỏ nhất không?
Vẽ hình:
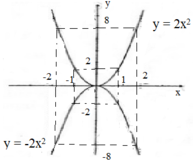
Nếu a > 0 thì hàm số đồng biến khi x > 0, nghịch biến khi x < 0
Với x = 0 thì hàm số đạt giá trị nhỏ nhất bằng 0. Không có giá trị nào của hàm số để đạt giá trị lớn nhất.
Nếu a < 0 thì hàm số đồng biến khi x < 0, nghịch biến khi x > 0.
Hàm số đạt giá trị lớn nhất y = 0 khi x = 0 . Không có giá trị bào của x để hàm số đạt giá trị nhỏ nhất.
cho hàm số bậc nhất y=(2-căn 5)x-2
a)hàm số trên đồng biến hay nghịch biến?vì sao?
b)tính giá trị của y khi x=2+căn 5
c)tính giá trị của x khi y=căn 5
Cho hàm số y=(1-√5)x-1
a, Hàm số đồng biến hay nghịch biến trên R?vì sao
Hàm số nghịch biến vi (1-√5<0
b,Tính y khi x=1+√5
y=(1-√5)(1+√5)-1
y = -5
Hãy vẽ đồ thị của các hàm số y = 2 x 2 , y = - 2 x 2 . Dựa vào đồ thị để trả lời các câu hỏi sau:
a) Nếu a > 0 thì hàm số y = a x 2 đồng biến khi nào? Nghịch biến khi nào?
Với giá trị nào của x thì hàm số đạt giá trị nhỏ nhất? Có giá trị nào của x để hàm số đạt giá trị lớn nhất không?
Nếu a < 0 thì hàm số đồng biến khi nào? Nghịch biến khi nào? Với giá trị nào của x thì hàm số đạt giá trị lớn nhất? Có giá trị nào của x để hàm số đạt giá trị nhỏ nhất không?
b) Đồ thị của hàm số y = a x 2 có những đặc điểm gì (trường hợp a > 0 , trường hợp a < 0)
Vẽ hình:
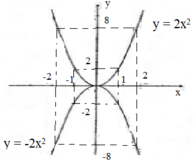
a) Nếu a > 0 thì hàm số đồng biến khi x > 0, nghịch biến khi x < 0
Với x = 0 thì hàm số đạt giá trị nhỏ nhất bằng 0. Không có giá trị nào của hàm số để đạt giá trị lớn nhất.
Nếu a < 0 thì hàm số đồng biến khi x < 0, nghịch biến khi x > 0.
Hàm số đạt giá trị lớn nhất y = 0 khi x = 0 . Không có giá trị bào của x để hàm số đạt giá trị nhỏ nhất.
b) Đồ thị hàm số y = a x 2 là đường cong (đặt tên là parabol) đi qua gốc tọa độ nhận trục tung Oy làm trục đối xứng.
Nếu a > 0 thì đồ thị nằm trên trục hoành, điểm O là điểm thấp nhất đồ thị (gọi là đỉnh parabol).
Nếu a < 0 thì đồ thị nằm bên dưới trục hoành, điểm O là điểm cao nhất của đồ thị.
Cho hàm số y = f(x) nghịch biến trên ℝ và thỏa mãn [f(x) - x]f(x) = x 6 + 3 x 4 + 2 x 2 , ∀ x ∈ ℝ . Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = f(x) trên đoạn [1;2]. Giá trị của 3M - m bằng
A. 4
B. -28
C. -3
D. 33
Chọn A
Ta có: ![]()
![]()
![]()
![]()
![]()
![]()
Với ![]() nên f(x) đồng biến trên
ℝ
nên f(x) đồng biến trên
ℝ
Với ![]() nên f(x) nghich biến trên
ℝ
nên f(x) nghich biến trên
ℝ
Suy ra: ![]() Vì f(x) nghich biến trên
ℝ
nên
Vì f(x) nghich biến trên
ℝ
nên 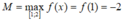 và
và ![]()
Từ đây ,ta suy ra: ![]()
=> chọn đáp án A
Câu 1: Cho hàm số y = (3m + 5) x\(^2\) với m \(\ne\) \(\dfrac{-5}{3}\). Tìm các giá trị của tham số m để hàm số:
a) Nghịch biến với mọi x > 0
b) Đồng biến với mọi x >0
c) Đạt giá trị lớn nhất là 0
d) Đạt giá trị nhỏ nhất là 0
Câu 2: Cho hàm số y = \(\left(\sqrt{3k+4}-3\right)x^2\) với k \(\ge\dfrac{-4}{3}\); k \(\ne\dfrac{5}{3}\)
Tính các giá trị của tham số K để hàm số:
a) Nghịch biến với mọi x >0
b) Đồng biến với mọi x >0
Câu 1:
a) Để hàm số \(y=\left(3m+5\right)\cdot x^2\) nghịch biến với mọi x>0 thì \(3m+5< 0\)
\(\Leftrightarrow3m< -5\)
hay \(m< -\dfrac{5}{3}\)
Vậy: Để hàm số \(y=\left(3m+5\right)\cdot x^2\) nghịch biến với mọi x>0 thì \(m< -\dfrac{5}{3}\)
b) Để hàm số \(y=\left(3m+5\right)\cdot x^2\) đồng biến với mọi x>0 thì
3m+5>0
\(\Leftrightarrow3m>-5\)
hay \(m>-\dfrac{5}{3}\)
Vậy: Để hàm số \(y=\left(3m+5\right)\cdot x^2\) đồng biến với mọi x>0 thì \(m>-\dfrac{5}{3}\)
2.
Để hàm nghịch biến với x>0 \(\Leftrightarrow\sqrt{3k+4}-3< 0\)
\(\Leftrightarrow\sqrt{3k+4}< 3\Leftrightarrow3k+4< 9\)
\(\Rightarrow-\dfrac{4}{3}\le k< \dfrac{5}{3}\)
Để hàm đồng biến khi x>0
\(\Leftrightarrow\sqrt{3k+4}-3>0\Leftrightarrow\sqrt{3k+4}>3\)
\(\Leftrightarrow3k+4>9\Rightarrow k>\dfrac{5}{3}\)