Chứng tỏ cặp phân thức sau bằng nhau:
3 2 x - 3 và 3 x + 6 2 x 2 + x - 6
Dùng tính chất cơ bản của phân thức chứng tỏ rằng các cặp phân thức sau bằng nhau: x 2 + 3 x + 2 3 x + 6 v à 2 x 2 + x - 1 6 x - 3
Cho cặp phân thức 9 x − 6 3 x 2 + 3 x − ( 2 x + 2 ) và 3 x 2 − 3 x + 3 x 3 + 1 với x ≠ − 1 và x ≠ 2 3 . Chứng tỏ cặp phân thức trên bằng nhau.
Chứng tỏ mỗi cặp phân thức sau bằng nhau
a) 2 2 p − 5 và 2 p + 4 2 p 2 − p − 10 , với p ≠ − 2 và p ≠ 5 2 ;
b) 3 q + 2 và 3 q 2 + 9 p q 3 + 5 q 2 + 6 q , với q ≠ − 3 và q ≠ − 2
a) 2 p + 4 2 p 2 − p − 10 = 2 ( p + 2 ) ( 2 p − 5 ) ( p + 2 ) = 2 2 p − 5
b) Tương tự câu a.
Chứng tỏ cặp phân thức sau bằng nhau:
2 x + 4 và 2 x 2 + 6 x x 3 + 7 x 2 + 12 x
Cách 1: Dùng định nghĩa hai phân thức bằng nhau:
2(x3 + 7x2 + 12x) = 2x3 + 14x2 + 24x
(x + 4)(2x2 + 6x) = 2x3 + 6x2 + 8x2 + 24x = 2x3 + 14x2 + 24x
⇒ 2(x3 + 7x2 + 12x) = (x + 4)(2x2 + 6x)
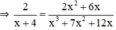
- Cách 2: Rút gọn phân thức:
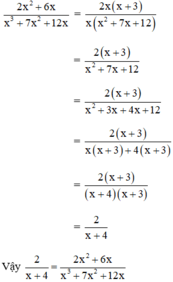
Dùng tính chất cơ bản của phân thức chứng tỏ rằng các cặp phân thức sau bằng nhau: 15 x - 10 3 x 2 + 3 x - 2 x + 2 v à 5 x 2 - 5 x + 5 x 3 + 1
Dùng tính chất cơ bản của phân thức chứng minh cặp phân thức sau bằng nhau x 2 + 3 x + 2 3 x + 6 và 2 x 2 + x - 1 6 x - 3
Chứng tỏ mỗi cặp phân thức sau bằng nhau :
a) \(\dfrac{3}{2x-3}\) và \(\dfrac{3x+6}{2x^2+x-6}\)
b) \(\dfrac{2}{x+4}\) và \(\dfrac{2x^2+6x}{x^3+7x^2+12x}\)
a) và
Cách 1: Dùng định nghĩa hai phân thức bằng nhau.
=
Vì :
=
=
=
Cách 2: Rút gọn phân thức
Dùng tính chấ cơ bản của phân thức chứng tỏ rằng các cặp phân thức sau bằng nhau :
a) \(\dfrac{x^2+3x+2}{3x+6}\) và \(\dfrac{2x^2+x-1}{6x-3}\)
b) \(\dfrac{15x-10}{3x^2+3x-\left(2x+2\right)}\) và \(\dfrac{5x^2-5x+5}{x^3+1}\)
a ) \(\dfrac{x^2+3x+2}{3x+6}=\dfrac{\left(x+1\right)\left(x+2\right)}{3\left(x+2\right)}=\dfrac{x+1}{3}\) (1)
\(\dfrac{2x^2+x-1}{6x-3}=\dfrac{\left(2x-1\right)\left(x+1\right)}{3\left(2x-1\right)}=\dfrac{x+1}{3}\) (2)
Từ (1) ; (2) \(\Rightarrow\dfrac{x^2+3x+2}{3x+6}=\dfrac{2x^2+x-1}{6x-3}\) (đpcm)
b ) \(\dfrac{15x-10}{3x^2+3x-\left(2x+2\right)}=\dfrac{5\left(3x-2\right)}{\left(3x-2\right)\left(x+1\right)}=\dfrac{5}{x+1}\) (3)
\(\dfrac{5x^2-5x+5}{x^3+1}=\dfrac{5\left(x^2-x+1\right)}{\left(x+1\right)\left(x^2-x+1\right)}=\dfrac{5}{x+1}\) (4)
Từ (3) và (4) \(\Rightarrow\dfrac{15x-10}{3x^2+3x-\left(2x+2\right)}=\dfrac{5x^2-5x+5}{x^3+1}\) (đpcm)
a) \(\dfrac{x^2+3x+2}{3x+6}=\dfrac{x^2+x+2x+2}{3\left(x+2\right)}=\dfrac{\left(x^2+x\right)+\left(2x+2\right)}{3\left(x+2\right)}=\dfrac{x\left(x+1\right)+2\left(x+1\right)}{3\left(x+2\right)}=\dfrac{\left(x+1\right)\left(x+2\right)}{3\left(x+2\right)}=\dfrac{x+1}{3}\left(1\right)\) \(\dfrac{2x^2+x-1}{6x-3}=\dfrac{2x^2+2x-x-1}{3\left(2x-1\right)}=\dfrac{2x\left(x+1\right)-\left(x+1\right)}{3\left(2x-1\right)}=\dfrac{\left(2x-1\right)\left(x+1\right)}{3\left(2x-1\right)}=\dfrac{x+1}{3}\left(2\right)\) Từ (1)và (2)=> \(\dfrac{x^2+3x+2}{3x+6}=\dfrac{2x^2+x-1}{6x-3}\) b)\(\dfrac{15x-10}{3x^2+3x-\left(2x+2\right)}=\dfrac{5\left(3x-2\right)}{3x\left(x+1\right)-2\left(x+1\right)}=\dfrac{5\left(3x-2\right)}{\left(3x-2\right)\left(x+1\right)}=\dfrac{5}{x+1}\left(3\right)\) \(\dfrac{5x^2-5x+5}{x^3+1}=\dfrac{5\left(x^2-x+1\right)}{\left(x+1\right)\left(x^2-x+1\right)}=\dfrac{5}{x+1}\left(4\right)\) Từ (3) và (4) => \(\dfrac{15x-10}{3x^2+3x-\left(2x+2\right)}=\dfrac{5x^2-5x+5}{x^3+1}\)
Bài 3 chứng tỏ các cặp phân số bằng sau đây bằng nhau:
a) -22/55 và -26/65
b) 25/53 và 2525/5353