Cho hai đường thẳng:
d: x = 6 y = - 2 t z = 7 + t và d 1 : x = - 2 + t ' y = - 2 z = - 11 - t '
Lập phương trình mặt phẳng (P) sao cho khoảng cách từ d và d 1 đến (P) là bằng nhau.
Những câu hỏi liên quan
Trong không gian Oxyz, cho hai đường thẳng
d
:
x
-
2
4
y
-
6
z
+
1
8
v
à
d
:
x
-
7
-
6
y...
Đọc tiếp
Trong không gian Oxyz, cho hai đường thẳng d : x - 2 4 = y - 6 = z + 1 8 v à d ' : x - 7 - 6 = y - 2 9 = z 12 . Trong các mệnh đề sau, mệnh đề nào đúng khi nói về vị trí tương đối của hai đường thẳng trên?
A. Song song
B. Chéo nhau
C. Song song
D. Cắt nhau
Chọn B.
Đường thẳng d có VTCP 
Đường thẳng d’ có VTCP 
Từ đó ta có:
Lại có:
Suy ra d và d’ chéo nhau.
Đúng 0
Bình luận (0)
Cho đường thẳng d: y = (m − 1)x + mvà d′: y = ( m 2 − 1)x + 6. Tìm m để hai đường thẳng d, d′ song song với nhau
A. m = 0 và m = 3
B. m = 0 và m = 2
C. m = 0 và m = 1
D. m = 0 và m = 4
Cho hai đường thẳng d: (m – 2)x +(m – 6)y + m – 1 0, ∆: (m – 4)x + (2m – 3)y – m + 5 0. Tất cả giá trị của m để hai đường thẳng cắt nhau là A.m ≠ 3 B.m ≠ 6 C.m ≠ 3 và m ≠ - 6 D.không có m thỏa mãn
Đọc tiếp
Cho hai đường thẳng d: (m – 2)x +(m – 6)y + m – 1= 0, ∆: (m – 4)x + (2m – 3)y – m + 5 = 0. Tất cả giá trị của m để hai đường thẳng cắt nhau là
A.m ≠ 3
B.m ≠ 6
C.m ≠ 3 và m ≠ - 6
D.không có m thỏa mãn
Xét hệ phương trình m − 2 x + m − 6 y = − m + 1 m − 4 x + 2 m − 3 y = m − 5 có định thức cấp hai là
D = m − 2 m − 6 m − 4 2 m − 3 = m − 2 . 2 m − 3 − m − 4 . m − 6
= m 2 + 3 m − 18 = m − 3 m + 6
Để hai đường thẳng cắt nhau thì hệ phương trình có nghiệm duy nhất
⟺ D ≠ 0 ⟺ m ≠ 3 m ≠ − 6
ĐÁP ÁN C
Đúng 0
Bình luận (0)
Cho các đường thẳng (d): y = 2x + 5m - 1 và đường thẳng (t): y = 4 - 3x. Tìm m để hai đường thẳng cắt nhau tại điểm A(x; y) có tọa độ thỏa mãn: x - 2y < 6
Tọa độ giao điểm là:
2x+5m-1=4-3x và y=4-3x
=>5x=4+1-5m và y=-3x+4
=>x=-m+1 và y=-3*(-m+1)+4=3m-3+4=3m+1
x-2y<6
=>-m+1-6m-3<6
=>-7m-2<6
=>-7m<8
=>m>-8/7
Đúng 0
Bình luận (0)
Cho hai đường thẳng
y
2
x
+
6
và
y
-
x
+
m
+
2
. Khi đó, giá trị của tham số m để hai đường thẳng cắt nhau tại một điểm trên trục tung là: A. m 4 B. m 3 C. m 2 D. m 1
Đọc tiếp
Cho hai đường thẳng y = 2 x + 6 và y = - x + m + 2 . Khi đó, giá trị của tham số m để hai đường thẳng cắt nhau tại một điểm trên trục tung là:
A. m = 4
B. m = 3
C. m = 2
D. m = 1
Đường thẳng y = 2 x + 6 cắt trục tung tại điểm A(0; 6) .
Để hai đường thẳng đã cho cắt nhau tại 1 điểm thuộc trục tung thì điểm A(0; 6) thuộc đường thẳng y = -x + m + 2 .
Suy ra 6 = m + 2 ⇔ m = 4 .
Đúng 0
Bình luận (0)
Cho đường thẳng d: y= (m-1) x+m và d’: y= (m2-1) x+ 6 . Có bao nhiêu giá trị của m để hai đường thẳng d; d’ song song với nhau.
A. 0
B. 1
C. 2
D. 3
Đáp án C
+Với m=1 ta có d: y=1 và d’: y=6
do đó hai đường thẳng này song song với nhau.
+ Với m =-1 ta có d: y= -2x-1 và d’: y= 6
suy ra hai đường thẳng này cắt nhau tại M(-7/2; 6)
+ Với m ≠ ± 1 khi đó hai đường thẳng trên là đồ thị của hàm số bậc nhất nên song song với nhau khi và chỉ khi:
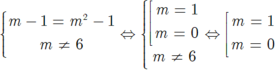
Đối chiếu với điều kiện m≠± 1 suy ra m= 0.
Vậy m= 0 và m= 1 là giá trị cần tìm.
Chọn C.
Đúng 0
Bình luận (0)
Trong không gian Oxyz, cho hai đường thẳng
△
:
x
-
1
-
2
y
+
2
1
z
-
3
2
và mặt phẳng (P): x+y-2z+60. Góc giữa đường thẳng
△
với mặt phẳng (P) bằn...
Đọc tiếp
Trong không gian Oxyz, cho hai đường thẳng △ : x - 1 - 2 = y + 2 1 = z - 3 2 và mặt phẳng (P): x+y-2z+6=0. Góc giữa đường thẳng △ với mặt phẳng (P) bằng
A. 30 °
B. 45 °
C. 60 °
D. 135 °
Bài tập 6. Trong mặt phẳng Oxy, cho hai đường thẳng
Delta_{1} / 2 * x - y - 2 0 , Delta_{2} / x - y + 3 0 và hai điểm A(-1;3) , B(0;2) .
a. Viết phương trình đường thẳng qua AB.
b. Viết phương trình đường thẳng trung trực của đoạn thẳng AB .
c. Viết phương trình đường thẳng qua 4 và song song với Delta_{1} .
d. Viết phương trình đường thẳng qua 4 và vuông góc với Delta_{1}
e. Viết phương trình đường thẳng qua B và có hệ số góc k - 3 . f. Tính côsin góc giữa hai đường thẳng Delta_{1}, De...
Đọc tiếp
Bài tập 6. Trong mặt phẳng Oxy, cho hai đường thẳng Delta_{1} / 2 * x - y - 2 = 0 , Delta_{2} / x - y + 3 = 0 và hai điểm A(-1;3) , B(0;2) . a. Viết phương trình đường thẳng qua AB. b. Viết phương trình đường thẳng trung trực của đoạn thẳng AB . c. Viết phương trình đường thẳng qua 4 và song song với Delta_{1} . d. Viết phương trình đường thẳng qua 4 và vuông góc với Delta_{1} e. Viết phương trình đường thẳng qua B và có hệ số góc k = - 3 . f. Tính côsin góc giữa hai đường thẳng Delta_{1}, Delta_{2} g. Tính d(A, Delta_{2}) . h. Viết phương trình đường thẳng qua 4 và tạo với Delta_{1} một góc c biết cos varphi = 1/(sqrt(5)) i. Tìm tọa độ hình chiếu vuông góc của 4 trên Delta_{2} j. Tìm tọa độ điểm B^ prime d hat oi xứng với B qua Delta_{2}
Trong không gian với hệ tọa độ Oxyz, cho điểm M (2;-1;-6) và hai đường thẳng
d
1
:
x
-
1
2
y
-
1
-
1
z
+
1
1
,
d...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho điểm M (2;-1;-6) và hai đường thẳng
d 1 : x - 1 2 = y - 1 - 1 = z + 1 1 , d 2 : x + 2 3 = y + 1 1 = z - 2 2 Đường thẳng đi qua điểm M và cắt cả hai đường thẳng d₁, d₂ tại hai điểm A, B. Độ dài đoạn thẳng AB bằng:
A. √38
B. 2√10
C. 8
D. 12
Chọn A
Vì A thuộc 
nên A (1+2t;1-t;-1+t).
Vì B thuộc 
nên B (-2+3t';-1+t';2+2t').
Thay vào (3) ta được t=1, t'=2 thỏa mãn.
Đúng 0
Bình luận (0)
Cho hai đường thẳng:
d
1
:
m
x
–
2
(
3
n
+
2
)
y
6
và
d
2
:
(
3
m
–
1
)
x
+
2
n
y...
Đọc tiếp
Cho hai đường thẳng: d 1 : m x – 2 ( 3 n + 2 ) y = 6 và d 2 : ( 3 m – 1 ) x + 2 n y = 56 . Tìm tích m.n để hai đường thẳng cắt nhau tại điểm I (−2; 3).
A. 0
B. 1
C. 2
D. −2
+) Thay tọa độ điểm I vào phương trình d 1 ta được:
m.(−2) – 2(3n + 2).3 = 6 ⇔ −2m – 18n = 18 ⇔ m + 9n = −9
+) Thay tọa độ điểm I vào phương trình d 2 ta được:
(3m – 1). (−2) + 2n.3 = 56 ⇔ −6m + 2 + 6n = 56 ⇔ m – n = −9
Suy ra hệ phương trình
m + 9 n = − 9 m − n = − 9 ⇔ m = − 9 + n − 9 + n + 9 n = − 9 ⇔ m = − 9 + n 10 n = 0
⇔ n = 0 m = − 9 ⇒ m . n = 0
Vậy m. n = 0
Đáp án: A
Đúng 0
Bình luận (0)