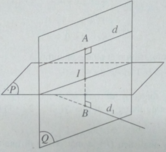
Đường thẳng d đi qua M(6; 0 ;7) có vecto chỉ phương a → (0; −2; 1). Đường thẳng d1 đi qua N(-2; -2; -11) có vecto chỉ phương b → (1; 0; −1).
Do d và d 1 chéo nhau nên (P) là mặt phẳng đi qua trung điểm của đoạn vuông góc chung AB của d, d 1 và song song với d và d 1 .
Để tìm tọa độ của A, B ta làm như sau:
Lấy điểm A(6; - 2t; 7 + t) thuộc d, B( -2 + t’; -2; -11 – t’) thuộc d 1 . Khi đó: AB → = (−8 + t′; −2 + 2t; −18 – t − t′)
Ta có: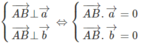 
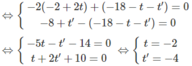
Suy ra A(6; 4; 5), B(-6; -2; -7)
Trung điểm của AB là I(0; 1; -1)
Ta có: AB → = (−12; −6; −12). Chọn n P → = (2; 1; 2)
Phương trình của (P) là: 2x + (y – 1) + 2(z + 1) = 0 hay 2x + y + 2z + 1 = 0.
Có thể tìm tọa độ của A, B bằng cách khác:
Ta có: Vecto chỉ phương của đường vuông góc chung của d và d 1 là:
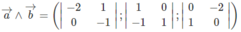= (2; 1; 2)
Gọi (Q) là mặt phẳng chứa d và đường vuông góc chung AB.
Khi đó:
n Q → = a → ∧ a → ∧ b →
Phương trình của (Q) là : –5(x – 6) + 2y + 4(z – 7) = 0 hay –5x + 2y + 4z + 2 = 0
Để tìm d 1 ∩ (Q) ta thế phương trình của d 1 vào phương trình của (Q). Ta có:
–5(–2 + t′) + 2(–2) + 4(–11 – t′) + 2 = 0
⇒ t′ = 4
⇒ d 1 ∩ (Q) = B(−6; −2; −7)
Tương tự, gọi (R) là mặt phẳng chứa d 1 và đường vuông góc chung AB. Khi đó: n R → = (−1; 4; −1)
Phương trình của (R) là –x + 4y – z – 5 = 0.
Suy ra d ∩ (R) = A(6; 4; 5).
