Giải bất phương trình sau x2 - x - 6 ≤ 0

Những câu hỏi liên quan
giải bất phương trình sau f(x)=(3x-4)(2x-3)/(x2-5x+6)(5-x)>0
\(f\left(x\right)=\dfrac{\left(3x-4\right)\left(2x-3\right)}{\left(x^2-5x+6\right)\left(5-x\right)}>0\)
\(\Leftrightarrow\dfrac{\left(3x-4\right)\left(2x-3\right)}{\left(x-2\right)\left(x-3\right)\left(5-x\right)}>0\)
Bảng xét dấu:
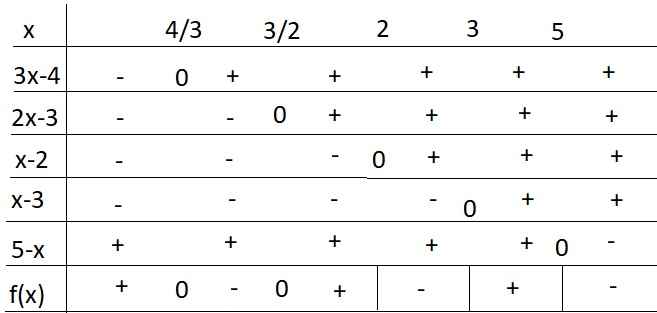
Từ bảng xét dấu ta thấy nghiệm của BPT là: \(\left[{}\begin{matrix}x< 5\\\dfrac{3}{2}< x< 2\\3< x< 5\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Giải các bất phương trình sau: ( x 2 / 3 ) + 3 x + 6 < 0 .
( x 2 / 3 ) + 3 x + 6 < 0 ⇔ x 2 + 9 x + 18 < 0 ⇔ -6 < x < -3
Đúng 0
Bình luận (0)
Giải bất phương trình sau:
x
2
-
x
-
2
x
2
-
x
-
1
≥
0
A. B. C. D.
Đọc tiếp
Giải bất phương trình sau:
x 2 - x - 2 x 2 - x - 1 ≥ 0
A. 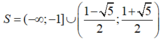
B. ![]()
C. 
D. 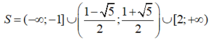
Chọn D
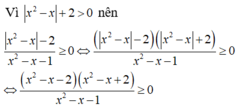
Bảng xét dấu
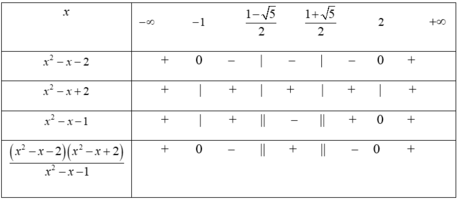
Dựa vào bảng xét dấu, ta có tập nghiệm của bất phương trình đã cho là
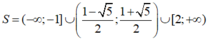
Đúng 0
Bình luận (0)
Giải bất phương trình:
x
2
+
1
-
x
+
1
x
2
+
3
x
-
6
≤...
Đọc tiếp
Giải bất phương trình:
x 2 + 1 - x + 1 x 2 + 3 x - 6 ≤ 0
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Chọn C
ĐKXĐ:
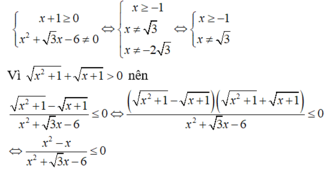
Bảng xét dấu
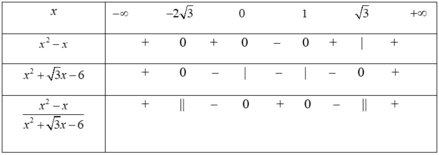
Dựa vào bảng xét dấu và đối chiếu điều kiện, ta có tập nghiệm của bất phương trình đã cho là
![]()
Đúng 0
Bình luận (0)
bài 1 giải các bất phương trình sau
a, -x2 +5x-6 ≥ 0
b, x2-12x +36≤0
c, -2x2 +4x-2≤0
d, x2 -2|x-3| +3x ≥ 0
e, x-|x+3| -10 ≤0
bài 2 xét dấu các biểu thức sau
a,<-x2+x-1> <6x2 -5x+1>
b, x2-x-2/ -x2+3x+4
c, x2-5x +2
d, x-< x2-x+6 /-x2 +3x+4 >
Bài 1:
a: \(\Leftrightarrow x^2-5x+6< =0\)
=>(x-2)(x-3)<=0
=>2<=x<=3
b: \(\Leftrightarrow\left(x-6\right)^2< =0\)
=>x=6
c: \(\Leftrightarrow x^2-2x+1>=0\)
\(\Leftrightarrow\left(x-1\right)^2>=0\)
hay \(x\in R\)
Đúng 0
Bình luận (0)
Giải bất phương trình sau: (x2 + 1)(x2 + 2)(x2 + 3)(x2 + 4) - 24 > 0
\(\Leftrightarrow\left(x^4+5x^2+6\right)\left(x^4+5x^2+4\right)-24\)
Đặt \(x^4+5x^2+6=t\)
\(t\left(t-2\right)-24=t^2-2t-24\)
\(\Leftrightarrow t^2-2t+1-25=\left(t-1\right)^2-5^2=\left(t-6\right)\left(t+4\right)>0\)
TH1 : \(\left\{{}\begin{matrix}t-6>0\\t+4>0\end{matrix}\right.\Leftrightarrow t>6\)
TH2 : \(\left\{{}\begin{matrix}t-6< 0\\t+4< 0\end{matrix}\right.\)<=> t < -4
Theo cách đặt \(x^4+5x^2+6>6\Leftrightarrow x^2\left(x^2+5\right)>0\)* luôn đúng *
\(x^4+5x^2+6< -4\Leftrightarrow x^4+5x^2+10< 0\)
\(\Leftrightarrow x^4+\dfrac{2.5}{2}x^2+\dfrac{25}{4}+\dfrac{15}{4}< 0\Leftrightarrow\left(x^2+\dfrac{5}{2}\right)^2+\dfrac{15}{4}< 0\)( vô lí )
Đúng 0
Bình luận (1)
Giải các bất phương trình sau: x 2 - 2 x + 3 > 0
x 2 - 2 x + 3 > 0 ⇔ ( x + 1 ) 2 + 2 > 0 (đúng với mọi x)
Đúng 0
Bình luận (0)
Giải bất phương trình
x2-2x+1<9
(x-1)(4-x2)≥0
\(\dfrac{x+2}{x-5}\)<0
\(x^2-2x+1< 9\)
\(\Leftrightarrow\left(x-1\right)^2< 9\)
\(\Leftrightarrow x-1< 3\)
\(\Leftrightarrow x< 4\)
\(\left(x-1\right)\left(4-x^2\right)\ge0\)
\(\Leftrightarrow\left(x-1\right)\left(2-x\right)\left(2+x\right)\ge0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\2-x=0\\2+x=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=2\\x=-2\end{matrix}\right.\)
\(\dfrac{x+2}{x-5}< 0\)
\(\Leftrightarrow x+2< 0\)
\(\Leftrightarrow x< -2\)
Đúng 0
Bình luận (0)
a)\(x^2-2x+1< 9\)
\(\Leftrightarrow\left(x-1\right)^2< 9\)
\(\Leftrightarrow\left(x-1\right)^2-9< 0\)
\(\Leftrightarrow\left(x-1-3\right)\left(x-1+3\right)< 0\)
\(\Leftrightarrow\left(x-4\right)\left(x+2\right)< 0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-4< 0\\x+2>0\end{matrix}\right.hay\left[{}\begin{matrix}x-4>0\\x+2< 0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x< 4\\x>-2\end{matrix}\right.hay\left[{}\begin{matrix}x>4\\x< -2\end{matrix}\right.\)(vô lý)
-Vậy nghiệm của BĐT là \(-2< x< 4\).
b) \(\left(x-1\right)\left(4-x^2\right)\ge0\)
\(\Leftrightarrow\left(x-1\right)\left(2-x\right)\left(x+2\right)\ge0\)
\(\Leftrightarrow\left(x-1\right)\left(x-2\right)\left(x+2\right)\le0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1< 0\\x-2>0\\x+2>0\end{matrix}\right.\) hay \(\left[{}\begin{matrix}x-1>0\\x-2< 0\\x+2>0\end{matrix}\right.\) hay \(\left[{}\begin{matrix}x-1>0\\x-2 >0\\x+2< 0\end{matrix}\right.\) hay \(\left[{}\begin{matrix}x-1< 0\\x-2< 0\\x+2< 0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x< 1\\x>2\\x>-2\end{matrix}\right.\) (vô lí) hay \(\left[{}\begin{matrix}x>1\\x< 2\\x>-2\end{matrix}\right.\) (có thể xảy ra) hay
\(\left[{}\begin{matrix}x>1\\x>2\\x< -2\end{matrix}\right.\) (vô lí) hay \(\left[{}\begin{matrix}x< 1\\x< 2\\x< -2\end{matrix}\right.\) (có thể xảy ra)
-Vậy nghiệm của BĐT là \(x< -2\) hay \(1< x< 2\).
c) ĐKXĐ: \(x\ne5\)
\(\dfrac{x+2}{x-5}< 0\Leftrightarrow\left[{}\begin{matrix}x+2< 0\\x-5>0\end{matrix}\right.hay\left[{}\begin{matrix}x+2>0\\x-5< 0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x< -2\\x>5\end{matrix}\right.\)(vô lí) hay
\(\left[{}\begin{matrix}x>-2\\x< 5\end{matrix}\right.\) (có thể xảy ra)
-Vậy nghiệm của BĐT là \(-2< x< 5\)
Đúng 0
Bình luận (1)
Giải các bất phương trình sau: x 2 + 1 x 2 + 3 x - 10 < 0














