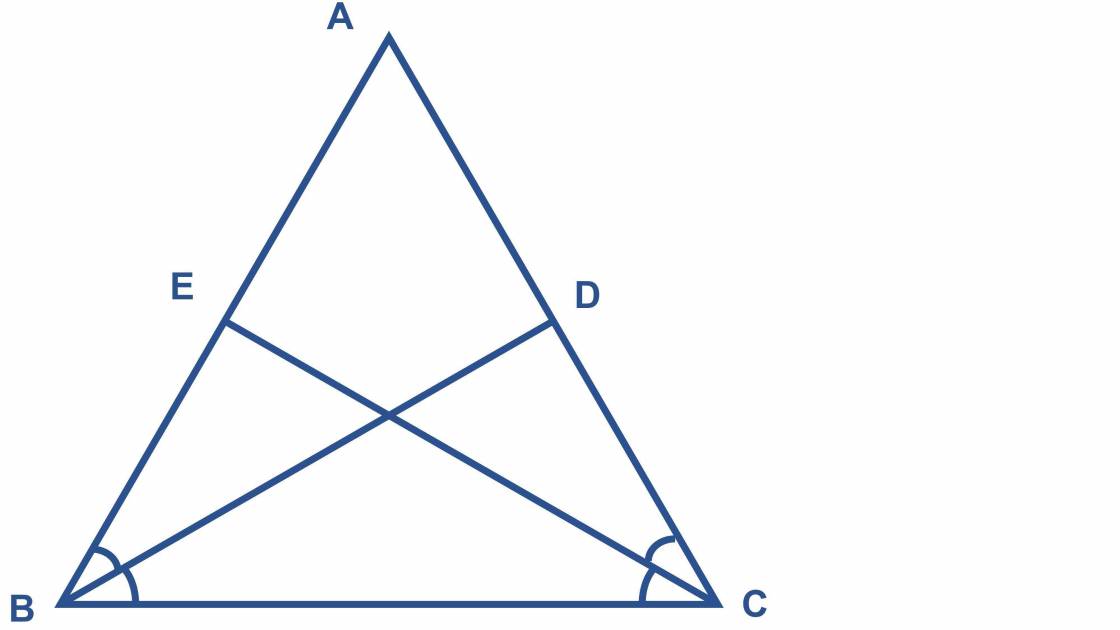
Cho tam giác ABC có hai đường trung tuyến BD, CE. Tính các tỉ số B G B D , C G C E và chứng minh B D + C E > 3 2 B C

Những câu hỏi liên quan
Bài 1: Cho tam giác ABC có 2 đường trung tuyến BD và CE
a) Tính các tỉ số \(\dfrac{BG}{BD}\) và \(\dfrac{CG}{CE}\)
b) Chứng minh rằng BD+CE> \(\dfrac{3}{2}BC\)
Mong mn giải giúp em ạ
a) ΔABC có 2 đường trung tuyến BD; CE
G là trọng tâm
=> BG/BD = 2/3
CG/CE = 2/3
b) Trong tam giác BGC ta có: BG + GC > BC
=> 2/3DB + 2/3CE > BC (G là trọng tâm)
=> 2/3(DB + CE) > BC
=> 3/2. 2/3 (DB+CE)> 3/2BC
=> (DB + CE)>3/2BC
Đúng 0
Bình luận (0)
Cho tam giác ABCcos hai đường trung tuyến bd, ce cắt nhau tại G
a,tính các tỉ số bg/ bd, Cg/ CE
b.cm bd+Ce>3/2 BC
Cho tam giác ABC có BC = 34 cm, đường trung tuyến BD = 24 cm, đường trung tuyến CE = 45 cm. Gọi G là giao điểm của BD và CE. Tính độ dài các cạnh của tam giác GDE
G là giao điểm của 2 đường trung tuyến BD và CE
Suy ra : G là trọng tâm tam giác ABC
Suy ra :
GD = 1/3 BD = 1/3 x 24 = 8 ( cm )
GE = 1/3 CE = 1/3 x 45 = 15 ( cm )
Xét tam giác ABC có :
E là trung điểm AB ( trung tuyến CE )
D là trung điểm AC ( trung tuyến BD )
Suy ra : ED là đường trung bình của tam giác ABC
Suy ra ED : = 1/2 x BC = 1/2 x 34 = 17 ( cm )
Vậy GD = 8 cm
GE = 15 cm
ED = 17 cm
Cho tam giác ABC cân tại A có hai đường trung tuyến BD và CE cắt nhau tại G . Biết BD = CE
a) Chứng minh tam giác GBC là tam giác cân
b) Chứng minh DG + EG > 1/2 BC
Câu này làm thế nào vậy mn
giúp mình với
Đúng 0
Bình luận (0)
xét ΔECB và ΔDBC, ta có :
EC = BD (gt)
\(\widehat{B}=\widehat{C}\) (2 góc đáy của ΔABC cân tại A)
BC là cạnh chung
=> ΔECB = ΔDBC (c.g.c)
=> \(\widehat{GBC}=\widehat{GCB}\) (2 góc tương ứng)
vì ΔGBC có \(\widehat{GBC}=\widehat{GCB}\) nên ⇒ ΔGBC là một tam giác cân (cân tại G)
Đúng 1
Bình luận (1)
Ví dụ 7. Cho tam giác ABC có các đường trung tuyến BD, CE cắt nhau tại G. Biết rằng BD = CE .
a) Tam giác GBC là tam giác gì? Vì sao?
b) Chứng minh ADBC =AECB.
c) Chứng minh tam giác ABC cân.
cho tam giác ABC có BD và CE là đường trung tuyến cắt nhau tại G. Biết BD=CE
a,chứng minh BG=CG;DG=GE
b,chứng minh tam giác ABC cân
cho tam giác ABC, các đường trung tuyến BD và CE. cho biết BC = 10cm, BD =9cm, CE = 12cm
a) chứng minh BD vuông góc với CE
b) tính diện tích tam giác ABC
Cho tam giác ABC vuông tại A có AB=6cm, AC=8cm. Vẽ trung tuyến AM
a. Tính số đo trung tuyến AM
b. Vẽ trung tuyến BD, CE, trọng tâm G. Tính số đo trung tuyến BD, CE
a: BC=10cm
=>AM=5cm
b: Vì D là trung điểm của AC
nên AD=4(cm)
=>\(BD=\sqrt{6^2+4^2}=2\sqrt{13}\left(cm\right)\)
Đúng 1
Bình luận (1)
cho tam giác ABC các đường trung tuyến BD,CE cho biết BC=10cm BD=9 cm CE=12 cm
chứng minh
â)BD vuông góc với CE
b)tính diện tích tam giác ABC
Gọi G là trọng tâm của tam giác ABC, khi đó ta có:
GC=23GE=23.12=8(cm)GC=23GE=23.12=8(cm)
GB=23BD=23.9=6(cm)GB=23BD=23.9=6(cm), ▲BGC có 102 = 62 + 82 hay BC2 = BG2 + CG2
=> ▲BGC vuông tại G hay BD vuông góc CE
Đúng 0
Bình luận (0)
Gọi G là trọng tâm của tam giác ABC, khi đó ta có:
GC=23GE=23.12=8(cm)GC=23GE=23.12=8(cm)
GB=23BD=23.9=6(cm)GB=23BD=23.9=6(cm), ▲BGC có 102 = 62 + 82 hay BC2 = BG2 + CG2
=> ▲BGC vuông tại G hay BD vuông góc CE
Đúng 0
Bình luận (0)