Vẽ đồ thị của các hàm số: y = √2;

Những câu hỏi liên quan
Cho hàm số y= 2+ x, vẽ đồ thị hàm số của y khi x = -2,-1,0,1,2,3
Cho hàm số y = 2 - x, vẽ đồ thị hàm số của y khi x = -2,-1,0,1,2,3
Cho hàm số y = x - 2, vẽ đồ thị hàm số của y khi x = -2,-1,0,1,2,3
Cho hàm số y = x + 2, vẽ đồ thị hàm số của y khi x = -2,-1,0,1,2,3
Cho hàm số y= 2+ x, vẽ đồ thị hàm số của y khi x = -2,-1,0,1,2,3
Cho hàm số y = 2 - x, vẽ đồ thị hàm số của y khi x = -2,-1,0,1,2,3
Cho hàm số y = x - 2, vẽ đồ thị hàm số của y khi x = -2,-1,0,1,2,3
Cho hàm số y = x + 2, vẽ đồ thị hàm số của y khi x = -2,-1,0,1,2,3
Từ đồ thị của hàm số y = 3 x , hãy vẽ đồ thị của các hàm số sau: y = 3x – 2
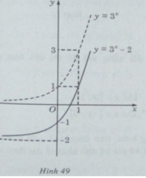
Đồ thị của hàm số y: y = 3 x − 2 nhận được từ đồ thị của hàm số y = 3 x bằng phép tịnh tiến song song với trục tung xuống dưới 2 đơn vị (H. 49)
Đúng 0
Bình luận (0)
Từ đồ thị của hàm số y = 3 x , hãy vẽ đồ thị của các hàm số sau: y = 2 – 3x
y = 2 – 3 x = −( 3 x − 2)
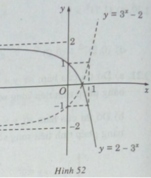
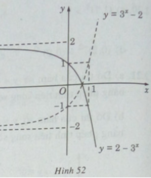
Ta có đồ thị của hàm số y = 2 − 3 x đối xứng với đồ thị cua hàm số y = 3 x – 2 qua trục hoành (H.52).
Đúng 0
Bình luận (0)
Từ đồ thị của hàm số y = 3 x , hãy vẽ đồ thị của các hàm số sau: y = 3x + 2
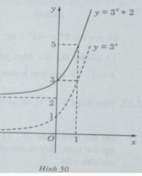
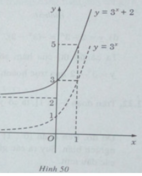
Đồ thị của hàm số y = 3 x + 2 nhận được từ đồ thị của hàm số y = 3 x bằng phép tịnh tiến song song với trục tung lên phía trên 2 đơn vị (H. 50)
Đúng 0
Bình luận (0)
Từ đồ thị của hàm số y = 3 x , hãy vẽ đồ thị của các hàm số sau: y = |3x – 2|
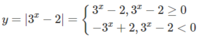
Do đó, đồ thị của hàm số y = | 3 x − 2| gồm:
- Phần đồ thị của hàm số y = 3 x − 2 ứng với 3 x – 2 ≥ 0 (nằm phía trên trục hoành).
- Phần đối xứng qua trục hoành của đồ thị hàm số y = 3 x − 2 ứng với 3 x – 2 < 0.
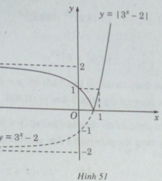
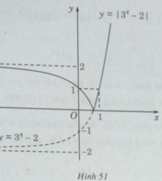
Vậy đồ thị của hàm số y = | 3 x − 2| có dạng như hình 51.
Đúng 0
Bình luận (0)
Từ đồ thị của hàm số y = 3 x , hãy vẽ đồ thị của các hàm số sau:
a) y = 3x – 2
b) y = 3x + 2
c) y = |3x – 2|
d) y = 2 – 3x
a) Đồ thị của hàm số y: y = 3 x − 2 nhận được từ đồ thị của hàm số y = 3 x bằng phép tịnh tiến song song với trục tung xuống dưới 2 đơn vị (H. 49)
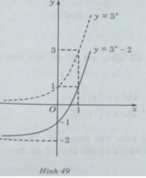
b) Đồ thị của hàm số y = 3 x + 2 nhận được từ đồ thị của hàm số y = 3 x bằng phép tịnh tiến song song với trục tung lên phía trên 2 đơn vị (H. 50)
c) 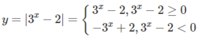
Do đó, đồ thị của hàm số y = | 3 x − 2| gồm:
- Phần đồ thị của hàm số y = 3 x − 2 ứng với 3 x – 2 ≥ 0 (nằm phía trên trục hoành).
- Phần đối xứng qua trục hoành của đồ thị hàm số y = 3 x − 2 ứng với 3 x – 2 < 0.
Vậy đồ thị của hàm số y = | 3 x − 2| có dạng như hình 51.
Ta có đồ thị của hàm số y = 2 − 3 x đối xứng với đồ thị cua hàm số y = 3 x – 2 qua trục hoành (H.52).
Đúng 0
Bình luận (0)
a) Vẽ đồ thị của hàm số: \(y = 0,5x;y = - 3x;y = x\).
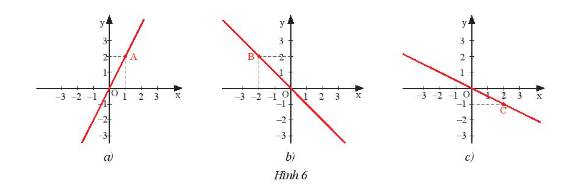
b) Các đồ thị sau đây là đồ thị của hàm số nào?
a)
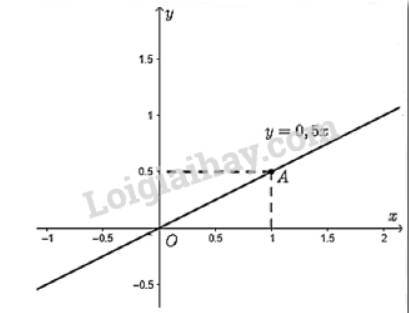
- Vẽ đồ thị hàm số \(y = 0,5x\)
Cho \(x = 1 \Rightarrow y = 0,5.1 = 0,5\). Ta vẽ điểm \(A\left( {1;0,5} \right)\)
Đồ thị hàm số \(y = 0,5x\) là đường thẳng đi qua điểm \(O\left( {0;0} \right)\) và \(A\left( {1;0,5} \right)\).
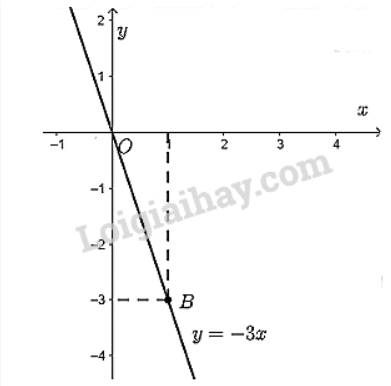
- Vẽ đồ thị hàm số \(y = - 3x\)
Cho \(x = 1 \Rightarrow y = - 3.1 = - 3\). Ta vẽ điểm \(B\left( {1; - 3} \right)\)
Đồ thị hàm số \(y = - 3x\) là đường thẳng đi qua điểm \(O\left( {0;0} \right)\) và \(B\left( {1; - 3} \right)\).
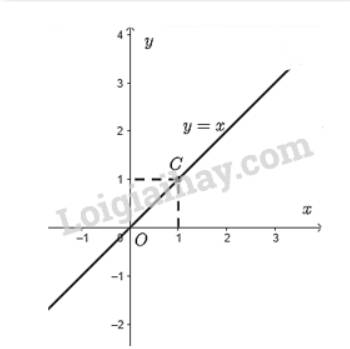
- Vẽ đồ thị hàm số \(y = x\)
Cho \(x = 1 \Rightarrow y = 1\). Ta vẽ điểm \(C\left( {1;1} \right)\)
Đồ thị hàm số \(y = x\) là đường thẳng đi qua điểm \(O\left( {0;0} \right)\) và \(C\left( {1;1} \right)\).
b) Ta thấy cả ba đồ thị đều đi qua gốc tọa độ \(O\left( {0;0} \right)\) nên có dạng \(y = ax\).
- Ở đồ thị a, đồ thị hàm số đi qua điểm \(A\left( {1;2} \right)\) nên ta có: \(2 = a.1 \Rightarrow a = 2\).
Do đó, đồ thị a là đồ thị của hàm số \(y = 2x\).
- Ở đồ thị b, đồ thị hàm số đi qua điểm \(B\left( { - 2;2} \right)\) nên ta có: \(2 = a.\left( { - 2} \right) \Rightarrow a = 2:\left( { - 2} \right) = - 1\).
Do đó, đồ thị b là đồ thị của hàm số \(y = - x\).
- Ở đồ thị c, đồ thị hàm số đi qua điểm \(C\left( {2; - 1} \right)\) nên ta có: \( - 1 = a.2 \Rightarrow a = \left( { - 1} \right):2 = \dfrac{{ - 1}}{2}\).
Do đó, đồ thị b là đồ thị của hàm số \(y = \dfrac{{ - 1}}{2}x\).
Đúng 0
Bình luận (0)
Câu 3: Cho các hàm số \(y=2x+5\) và \(y=-x+2\)
a. Vẽ đồ thị của hai hàm số đã cho trên cùng một mặt phẳng toạ độ Oxy.
b. Dựa vào hình vẽ, xác định toạ độ giao điểm A của hai đồ thị hàm số.
c. Hai đồ thị của hai hàm số đã cho cắt trục hoành tại các điểm B và C. Tính diện tích tam giác ABC
\(b,\text{PT hoành độ giao điểm: }2x+5=-x+2\Leftrightarrow3x=-3\\ \Leftrightarrow x=-1\Leftrightarrow y=3\Leftrightarrow A\left(-1;3\right)\\ c,\text{PT 2 đt giao Ox: }\left\{{}\begin{matrix}y=0\Rightarrow x=-\dfrac{5}{2}\Rightarrow B\left(-\dfrac{5}{2};0\right)\\y=0\Rightarrow x=2\Rightarrow C\left(2;0\right)\end{matrix}\right.\\ \Rightarrow BC=OB+OC=\dfrac{5}{2}+2=\dfrac{9}{2}\\ \text{Gọi H là chân đường cao từ A tới BC}\\ \Rightarrow AH=\left|y_A\right|=3\\ \Rightarrow S_{ABC}=\dfrac{1}{2}AH\cdot BC=\dfrac{1}{2}\cdot3\cdot\dfrac{9}{2}=\dfrac{27}{4}\left(đvdt\right)\)
Đúng 1
Bình luận (0)
Bài 1.cho hàm số y= 4/5.x
a)vẽ đồ thị hàm số
b)tìm giá trị của hàm số tại x=(-1);x=0
bài 2. cho hàm số y=-2/5.x
a)vẽ đồ thị hàm số
b)trong các điểm sau đây thì điểm nào thuộc đồ thị hàm số đó:M(-5;2);N(0;3);P(3;hỗn số -1,1/5)












