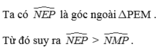Cho tam giác MNP, E là một điểm trên MN. Chứng minh: N E P ^ > N M P ^

Những câu hỏi liên quan
Cho tam giác MNP vuông tại M, trung tuyến MI. Trên tia MI lấy điểm Q sao cho MQ=2MI. Chứng minh NQ//MP. Chứng minh tam giác MNP=tam giác NMQ. Gọi G là trọng tâm của tam giác MNQ. Tính IG biết MN =9cm, NQ = 12cm. Trên tia MQ lấy điểm K sao cho MQ = 3MK. Gọi E là trung điểm của MP. Chứng minh N,K, thẳng hàng
Cho tam giác MNP vuông ở M, đường cao MH, phân giác góc MNP cắt MP tại D. Cho biết MN = 6cm, MP = 8cm. a) Tính NP. Chứng minh Δ H M N và Δ H P M đồng dạng. b) Trên NP lấy điểm E sao cho PE = 4cm. Chứng minh N E 2 = N H . N P c) Tính diện tích Δ P E D
Cho tam giác MNP, E là một điểm trên MN. Chứng minh: N E P ^ > N M P ^
Cho tam giác MNP vuông tại M, đường cao MH a) chứng minh tam giác HNM đồng dạng tam giác MNP b) chứng minh hệ thức MH²= NH.PH c) Lấy điểm E tùy ý trên cạnh MP ( E khác M,P) .vẽ điểm F trên cạnh MN sao cho góc FHE = 90°. Chứng minh tam giác NFH đồng dạng tam giác MEH và góc NMH = góc FEH. d) xác định vị trí của điểm E trên MP sao cho diện tích tam giác HÈ đạt giá trị nhỏ nhất
a: Xét ΔHNM vuông tại H và ΔMNP vuông tại M có
góc N chung
=>ΔHNM đồng dạng với ΔMNP
b: ΔMNP vuông tại M co MH vuông góc NP
nên MH^2=HN*HP
Đúng 1
Bình luận (0)
Tình trang gấp 1 ngày nữa thôi ai giải hộ mình bài này:Cho tam giác MNP vuông tại M, trung tuyến MI. Trên tia MI lấy điểm Q sao cho MQ 2MI :a) Chứng minh NQ//MPb) Chứng minh tam giác MNP tam giác NMQc) Gọi G là trọng tâm của tam giác MNQ. Tính IG biết MN9cm, NQ12cmd) Trên tia MQ lấy điểm K sao cho MQ3MK. Gọi E là trung điểm của MP . Chứng minh N, K, E thẳng hàngMình cảm ơn trước
Đọc tiếp
Tình trang gấp 1 ngày nữa thôi ai giải hộ mình bài này:
Cho tam giác MNP vuông tại M, trung tuyến MI. Trên tia MI lấy điểm Q sao cho MQ =2MI :
a) Chứng minh NQ//MP
b) Chứng minh tam giác MNP = tam giác NMQ
c) Gọi G là trọng tâm của tam giác MNQ. Tính IG biết MN=9cm, NQ=12cm
d) Trên tia MQ lấy điểm K sao cho MQ=3MK. Gọi E là trung điểm của MP . Chứng minh N, K, E thẳng hàng
Mình cảm ơn trước
cho tam giác MNP có MNMP, MI là đường trung tuyến.a) tam giác MNP là tam giác gì?b)chứng minh: tam giác MNI tam giác MPIc) chứng minh MI là dường trung trực của đoạn thẳng NPd) cho MNMP 10cm, NP 12cm. tính độ dài MIe)kẻ IH vuông góc với MN, H thuộc MN. trên MH lấy điểm E, trên MH lấy điểm E, trên MP lấy điểm Fsao cho góc MEF bằng hai lần góc EIH. chứng minh rằng: EI là tia phân giác của góc HEF
Đọc tiếp
cho tam giác MNP có MN=MP, MI là đường trung tuyến.
a) tam giác MNP là tam giác gì?
b)chứng minh: tam giác MNI= tam giác MPI
c) chứng minh MI là dường trung trực của đoạn thẳng NP
d) cho MN=MP= 10cm, NP= 12cm. tính độ dài MI
e)kẻ IH vuông góc với MN, H thuộc MN. trên MH lấy điểm E, trên MH lấy điểm E, trên MP lấy điểm Fsao cho góc MEF bằng hai lần góc EIH. chứng minh rằng: EI là tia phân giác của góc HEF
a) tam giác MNP có MN=MP(GT) suy ra tam giác MNP cân tại M (ĐỊNH nghĩa tam giác cân)
b) xét tam giác MNI và MPI có
MI chung
MN=MP(GT)
IN=IP(MI là trung tuyến nên I là trung điểm NP)
SUY ra tam giác MNI=MPI(C-C-C)
c) Vì tam giác MNP cân tại M(cmt)màMI là đường trung tuyến nên MI đồng thời cũng là đường cao đường trung trực hay MI là đường trung trực của NP (tính chất tam giác cân)
d)Vì MI là đường cao tam giác MNP(cmt) suy ra MI vuông góc với NP suy ra tam giác MNI vuông tại I
Vì MI là đường trung tuyến nên I là trung điểm NP suy ra NI=1/2NP
Mà NP=12cm(gt) suy ra NI=12x1/2=6cm
xét tam giác vuông MNI có
NM2=NI2+MI2(ĐỊNH LÍ Py-ta-go)
Suy ra MI2=NM2-NI2
mà NM=10CM(gt) NI=6CM(cmt)
suy ra MI2=102-62=100-36=64=căn bậc 2 của 64=8
mà MI>0 Suy ra MI=8CM (đpcm)
ế) mik gửi cho bn bằng này nhé
Đúng 0
Bình luận (0)
a) Vì MN=MP => tam giác MNP là tam giác cân tại M.
b)Xét tam giác MIN và tam giác MIP có:
MN=MP (vì tam giác MNP cân)
\(\widehat{MNP}=\widehat{MPI}\)(tam giác MNP cân)
NI=PI(vì MI là trung tuyến)
=> tam giác MIN=tam giác MIP(c.g.c)
c) Ta có: MN=MP
IN=IP
=> M,I thuộc trung trực của NP
Hay MI là đường trung trực của NP
d) IN=IP=NP/2=12/2=6(cm)
Xét tam giác MIN có góc MIN =90*
=> MN^2=MI^2 + NI^2
=> MI^2=MN^2-NI^2
=> MN^2 = 10^2 - 6^2
=> MN = 8
e) Tam giác HEI có goc IHE=90*
=> góc HEI + góc HIE= 90*
Mà góc HIE = góc MEF/2
=> góc MEF/2 + góc HEI = 90* (1)
Mà góc MEF + góc HEI + góc IEF = 180*
=> góc MEF/2 + góc IEF = 90* (2)
Từ (1) và (2) => góc HEI = góc IEF
Hay EI là tia phân giác của góc HEF
Đúng 0
Bình luận (0)
cảm ơn hoàng hàn nhật băng nhiều, mk mới tham gia nên ko biết mỗi câu hỏi chỉ dc k đúng 1 lần xin lỗi bạn nha
Đúng 0
Bình luận (0)
Cho tam giác MNP vuông tại M có MN 3cm. MP 4cm.a) Tính độ dài NP.b) Trên tia MN lấy điểm D sao cho N là trung điểm của MD. Từ N vẽ đường thẳng vuông góc với MD cắt PD tại E. Chứng minh rằng tam giác MDE cân tại E.c) Trên tia đối của tia EM lấy điểm F sao cho EM EF. Từ F kẻ FI vuông góc với NE tại I. Chứng minh rằng FI ND.d) Chứng minh 3 điểm F, I, P thẳng hàng.
Đọc tiếp
Cho tam giác MNP vuông tại M có MN = 3cm. MP = 4cm.
a) Tính độ dài NP.
b) Trên tia MN lấy điểm D sao cho N là trung điểm của MD. Từ N vẽ đường thẳng vuông góc với MD cắt PD tại E. Chứng minh rằng tam giác MDE cân tại E.
c) Trên tia đối của tia EM lấy điểm F sao cho EM = EF. Từ F kẻ FI vuông góc với NE tại I. Chứng minh rằng FI = ND.
d) Chứng minh 3 điểm F, I, P thẳng hàng.
a: NP=5cm
b: Xét ΔEMD có
EN là đường cao
EN là đường trug tuyến
Do đó: ΔEMD cân tại E
Đúng 1
Bình luận (0)
cho tam giac MNP vuông tại M( MN>MP). trên cạnh NP lấy điểm E sao cho NE = NM, qua E kẻ đừơng thăng vuông góc với NP cắt MP tại D
a) chứng minh tam giác MND = tam giác END và ND phân giác của MNP
b) trên tia đối của tia MN, lấy điểm F sao cho MF = DP chứng minh tam giác MDF= tam giác EDP
c) minh 3 điểm E , D , F thẳng hàng
d) chứng m ND vuông góc với CF
Cho tam giác MNP vuông cân tại M, vẽ đường cao MH ( H thuộc NP) . Trên cạnh MN và MP lần lượt lấy hai điểm D và E (D khác M,N và E khác M,P) sao cho MD = ME, gọi K là một điểm thuộc đoạn NH (K khác N). Trên nửa mặt phẳng bờ là Mp không chứa điểm N vẽ điểm I sao cho \(\widehat{IME}=\widehat{KMD}\)và MI = MK. Chứng minh \(KE+KD\ge MN\)
Hình vẽ bạn tự vẽ nha
Trước hết chứng minh :(tự chứng minh lun)
Cho tam giác ABC vuông cân tại A . Chứng minh \(\sqrt{2}\cdot AB=BC\)(*)
Xét tam giác KDM và tam giác IEM ta có:
KM=MI (gt)
KMD= IME (gt);
MD=ME (gt);
=> tam giác KDM = tam giác IEM (c.g.c);
=> KD= EI (tương ứng);
Lại có NMP=90 (gt) => NMK+ KMP=90
=> IME+ KMP =90 => IMK =90 mà KM=MI
=> tam giác KMI vuông cân tại M
Xét tam giác NMP vuông cân tại M có MNH=45 mà MHN=90 (do MH là đường cao)
=>Tam giác MHN vuông cân tại H
Áp dụng (*) vào tam giác KMI vuông cân tại M và tam giác MHN vuông cân tại H ta được:
\(\hept{\begin{cases}\sqrt{2}\cdot MH=MN\\\sqrt{2}\cdot KM=KI\end{cases}}\)mà \(KM\ge MH\)
\(\Rightarrow KI\ge MN\)
Xét 3 điểm K,E,I ta có:
\(KE+EI\ge KI\)
hay \(KE+KD\ge MN\)
Hoàng Nguyễn Văn Dòng thứ 5 dưới lên sai rồi mem,tự coi lại nha,không thể như thế được đâu.Tại sao \(KM\ge MH\) lại suy ra \(KI\ge MN\) được ??
nhân cả 2 vế với căn 2 thui mà