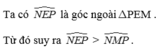Các câu hỏi tương tự
Cho tam giác MNP vuông tại M, trung tuyến MI. Trên tia MI lấy điểm Q sao cho MQ=2MI. Chứng minh NQ//MP. Chứng minh tam giác MNP=tam giác NMQ. Gọi G là trọng tâm của tam giác MNQ. Tính IG biết MN =9cm, NQ = 12cm. Trên tia MQ lấy điểm K sao cho MQ = 3MK. Gọi E là trung điểm của MP. Chứng minh N,K, thẳng hàng
Cho tam giác MNP, E là một điểm trên MN. Chứng minh: N E P ^ > N M P ^
Tình trang gấp 1 ngày nữa thôi ai giải hộ mình bài này:Cho tam giác MNP vuông tại M, trung tuyến MI. Trên tia MI lấy điểm Q sao cho MQ 2MI :a) Chứng minh NQ//MPb) Chứng minh tam giác MNP tam giác NMQc) Gọi G là trọng tâm của tam giác MNQ. Tính IG biết MN9cm, NQ12cmd) Trên tia MQ lấy điểm K sao cho MQ3MK. Gọi E là trung điểm của MP . Chứng minh N, K, E thẳng hàngMình cảm ơn trước
Đọc tiếp
Tình trang gấp 1 ngày nữa thôi ai giải hộ mình bài này:
Cho tam giác MNP vuông tại M, trung tuyến MI. Trên tia MI lấy điểm Q sao cho MQ =2MI :
a) Chứng minh NQ//MP
b) Chứng minh tam giác MNP = tam giác NMQ
c) Gọi G là trọng tâm của tam giác MNQ. Tính IG biết MN=9cm, NQ=12cm
d) Trên tia MQ lấy điểm K sao cho MQ=3MK. Gọi E là trung điểm của MP . Chứng minh N, K, E thẳng hàng
Mình cảm ơn trước
cho tam giác MNP có MNMP, MI là đường trung tuyến.a) tam giác MNP là tam giác gì?b)chứng minh: tam giác MNI tam giác MPIc) chứng minh MI là dường trung trực của đoạn thẳng NPd) cho MNMP 10cm, NP 12cm. tính độ dài MIe)kẻ IH vuông góc với MN, H thuộc MN. trên MH lấy điểm E, trên MH lấy điểm E, trên MP lấy điểm Fsao cho góc MEF bằng hai lần góc EIH. chứng minh rằng: EI là tia phân giác của góc HEF
Đọc tiếp
cho tam giác MNP có MN=MP, MI là đường trung tuyến.
a) tam giác MNP là tam giác gì?
b)chứng minh: tam giác MNI= tam giác MPI
c) chứng minh MI là dường trung trực của đoạn thẳng NP
d) cho MN=MP= 10cm, NP= 12cm. tính độ dài MI
e)kẻ IH vuông góc với MN, H thuộc MN. trên MH lấy điểm E, trên MH lấy điểm E, trên MP lấy điểm Fsao cho góc MEF bằng hai lần góc EIH. chứng minh rằng: EI là tia phân giác của góc HEF
cho tam giac MNP vuông tại M( MN>MP). trên cạnh NP lấy điểm E sao cho NE = NM, qua E kẻ đừơng thăng vuông góc với NP cắt MP tại D
a) chứng minh tam giác MND = tam giác END và ND phân giác của MNP
b) trên tia đối của tia MN, lấy điểm F sao cho MF = DP chứng minh tam giác MDF= tam giác EDP
c) minh 3 điểm E , D , F thẳng hàng
d) chứng m ND vuông góc với CF
Cho tam giác MNP vuông cân tại M, vẽ đường cao MH ( H thuộc NP) . Trên cạnh MN và MP lần lượt lấy hai điểm D và E (D khác M,N và E khác M,P) sao cho MD = ME, gọi K là một điểm thuộc đoạn NH (K khác N). Trên nửa mặt phẳng bờ là Mp không chứa điểm N vẽ điểm I sao cho \(\widehat{IME}=\widehat{KMD}\)và MI = MK. Chứng minh \(KE+KD\ge MN\)
1. Cho tam giác MNP cân tại M vẽ MH thuộc NP (H thuộc NP)a) Chứng minh NH PHb) Cho MH 4 cm; NH 3 cm. Tính MN2. Cho tam giác MNP vuông tại M, có góc N 60o và MN 5 cm. Tia phân giác của góc N cắt MP tại D. Kẻ DE vuông góc với PN tại Ea) Chứng minh: tam giác MNP tam giác ENDb) Chứng minh: tam giác MNE là tam giác đềuc) Tính độ dài cạnh PN3. Cho tam giác MNP cân tại M, góc M 30o; NP 2 cm. Trên cạnh MP lấy điểm Q sao cho góc PNQ 60o. Tính độ dài MQ
Đọc tiếp
1. Cho tam giác MNP cân tại M vẽ MH thuộc NP (H thuộc NP)
a) Chứng minh NH = PH
b) Cho MH = 4 cm; NH = 3 cm. Tính MN
2. Cho tam giác MNP vuông tại M, có góc N = 60o và MN = 5 cm. Tia phân giác của góc N cắt MP tại D. Kẻ DE vuông góc với PN tại E
a) Chứng minh: tam giác MNP = tam giác END
b) Chứng minh: tam giác MNE là tam giác đều
c) Tính độ dài cạnh PN
3. Cho tam giác MNP cân tại M, góc M = 30o; NP = 2 cm. Trên cạnh MP lấy điểm Q sao cho góc PNQ = 60o. Tính độ dài MQ
Cho tam giác MNP vuông tại M. Trên cạnh NP lấy điểm E sao cho NE=MN. Tia phân giác của góc N cắt MP ở D.
a) So sánh DM và DE, tính góc NED
b) Tia ED cắt tia đối của tia MN tại K. Chứng minh tam giác DMK= tam giác DEP
c) Chứng minh ND vuông góc với KP
Cho tam giác MNP vuông tại M, góc N= 60 độ , MN= 5cm. Tia phân giác góc N cắt MP tại D, từ D kẻ đường thẳng vuông góc với MN tại E
a) Chứng minh tam giác NMD= tam giác NED
b) Chứng minh tam giác MND là tam giác đều