Viết phương trình của dao động điều hòa và giải thích các đại lượng trong phương trình.
Những câu hỏi liên quan
Viết phương trình của dao động điều hòa và giải thích các đại lượng trong phương trình.
Phương tridnh dao động điều hòa là x = Acos(ωt+ Ø), trong đó:
- x là li độ của dao động
- A là biên độ dao động
- ω là tần số góc của đơn vị, có đơn vị là rad/s
- (ωt+ Ø) là pha của dao động tại thời điểm t, có đơn vị là rad,
- Ø là pha ban đầu của dao động
Đúng 0
Bình luận (0)
Phương trình dao động điều hòa
x=Acos(\(\omega\)t + \(\varphi\))
Trong đó x là li độ,
A là biên độ,
(\(\omega\)t + \(\varphi\)) là pha dao động (thường dùng đơn vị rad),
\(\varphi\) là pha ban đầu,
\(\omega\) là tần số góc (thường dùng đơn vị rad/s).
Đúng 0
Bình luận (0)
Trong phương trình dao động điều hòa , đại lượng được gọi là: A. biên độ dao động B. tần số dao động C. pha dao động D. chu kì dao động
Đọc tiếp
Trong phương trình dao động điều hòa 
, đại lượng 
được gọi là:
A. biên độ dao động
B. tần số dao động
C. pha dao động
D. chu kì dao động
SGK Kết nối tri thức với cuộc sống - Trang 10
14 tháng 7 2023 lúc 22:59
Để vẽ đồ thị hoặc viết phương trình của một dao động điều hòa cần biết những đại lượng vật lí nào?
Ta có: `x=Acos(\omega t+\pi/2)`
`=>` Để vẽ đồ thị hoặc viết phương trình của một dao động điều hòa cần những đại lượng vật lí là:
+, `A` là biên độ dao động `(m;cm;mm;....)`
+, `\omega` là tần số góc của dao động `(rad//s)`
+, `\varphi` là pha ban đầu của dao động `(rad)`.
Đúng 1
Bình luận (0)
Một vật có khối lượng m 100 g thực hiện dao động là dao động tổng hợp của hai dao động điều hòa cùng phương có phương trình lân lượt là
x
1
6
cos
(
10
t
+
0
,
5
π
)
(cm) và
x
2
10
cos
(
10
t
-...
Đọc tiếp
Một vật có khối lượng m = 100 g thực hiện dao động là dao động tổng hợp của hai dao động điều hòa cùng phương có phương trình lân lượt là x 1 = 6 cos ( 10 t + 0 , 5 π ) (cm) và x 2 = 10 cos ( 10 t - 0 , 5 π ) (cm) (t tính bằng s). Động năng cực đại của vật trong quá trình dao động bằng
A. 160J.
B. 16 mJ.
C. 8 mJ.
D. 80J
Một vật có khối lượng m 100 g thực hiện dao động là dao động tổng hợp của hai dao động điều hòa cùng phương có phương trình lân lượt là
x
1
6
cos
10
t
+
0
,
5
π
(cm) và
x
2
10
cos
10
t...
Đọc tiếp
Một vật có khối lượng m = 100 g thực hiện dao động là dao động tổng hợp của hai dao động điều hòa cùng phương có phương trình lân lượt là x 1 = 6 cos 10 t + 0 , 5 π (cm) và x 2 = 10 cos 10 t - 0 , 5 π (cm) (t tính bằng s). Động năng cực đại của vật trong quá trình dao động bằng
A. 160J.
B. 16 mJ.
C. 8 mJ.
D. 80J.
Cho và là hai phương trình của hai dao động điều hòa cùng phương. Biết phương trình của dao động tổng hợp là . Để tổng biên độ của các dao động thành phần (A1 + A2) cực đại thì φ có giá trị là: A. π/6 B. π/24 C. 5π/12 D. π/12
Đọc tiếp
Cho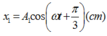 
và 
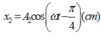là hai phương trình của hai dao động điều hòa cùng phương. Biết phương trình của dao động tổng hợp là 
. Để tổng biên độ của các dao động thành phần (A1 + A2) cực đại thì φ có giá trị là:
A. π/6
B. π/24
C. 5π/12
D. π/12
Đáp án B
Phương pháp: Sử dụng giản đồ vecto và định lí hàm số sin trong tam giác
Cách giải:
- Phương trình dao động của x; x1; x2: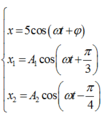 
Suy ra :
+ Độ lệch pha giữa x và x1 là :
+ Độ lệch pha giữa x và x2 là :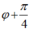 
+ Độ lệch pha giữa x1 và x2 là :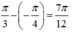 
=> Ta có giản đồ vecto :
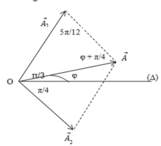
- Áp dụng định lí hàm số sin trong tam giác ta có:
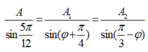
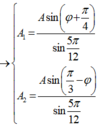
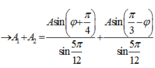
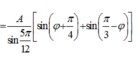
có: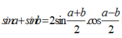
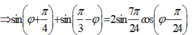
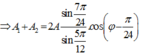
Để [A1 + A2] đạt cực đại thì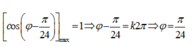 
Đúng 0
Bình luận (0)
Trong phương trình dao động điều hòa , đại lượng thay đổi theo thời gian là:
A. tần số góc ω .
B. pha ban đầu
C. biên độ A
D. li đô x
+ Các đại lượng A, ω và φ là hằng số (A và ω luôn dương)
+ từ đề thấy x phụ thuộc vào t theo dạng hàm số cos => Chọn D.
Đúng 0
Bình luận (0)
Trong một dao động điều hòa có phương trình:
x
A
cos
ω
t
+
φ
, rad/s là đơn vị của đại lượng nào? A. Chu kì dao động T. B. Tần số góc ω. C. Biên độ A D. Pha dao động (ωt+φ)
Đọc tiếp
Trong một dao động điều hòa có phương trình: x = A cos ω t + φ , rad/s là đơn vị của đại lượng nào?
A. Chu kì dao động T.
B. Tần số góc ω.
C. Biên độ A
D. Pha dao động (ωt+φ)
Trong một dao động điều hòa có phương trình:
x
Acos
ω
+
φ
, rad/s là đơn vị của đại lượng nào? A. Chu kì dao động T B. Tần số góc ω C. Biên độ A D. Pha dao động (ωt+φ)
Đọc tiếp
Trong một dao động điều hòa có phương trình: x = Acos ω + φ , rad/s là đơn vị của đại lượng nào?
A. Chu kì dao động T
B. Tần số góc ω
C. Biên độ A
D. Pha dao động (ωt+φ)