D={1;2;3;4;5;6;7;8;9} bằng cách chỉ ra đặc trưng của các phần tử trong tập hợp:

Những câu hỏi liên quan
cho a+b+c+d =2000 và 1/a+b+c+1/b+c+d+1/c+d+a +1/d+a+b=1/40
tính giá trị S= a/b+c+d+b/c+d+a +c/d+a+b+d/a+b+c
Em có cách khác!
\(\frac{1}{a+b+c}+\frac{1}{b+c+d}+\frac{1}{c+d+a}+\frac{1}{d+a+b}=\frac{1}{40}\)
\(\Rightarrow\frac{a+b+c+d}{a+b+c}+\frac{a+b+c+d}{b+c+d}+\frac{a+b+c+d}{c+d+a}\)
\(+\frac{a+b+c+d}{d+a+b}=50\)
\(\Rightarrow\frac{d}{a+b+c}+1+\frac{a}{b+c+d}+1+\frac{b}{c+d+a}+1\)
\(+\frac{c}{d+a+b}+1=50\)
\(\Rightarrow\frac{d}{a+b+c}+\frac{a}{b+c+d}+\frac{b}{c+d+a}+\frac{c}{d+a+b}=46\)
Đề: \(a+b+c+d=2000\)
\(\frac{1}{a+b+c}+\frac{1}{b+c+d}+\frac{1}{c+d+a}+\frac{1}{d+a+b}=\frac{1}{40}\)
Tính:
\(S=\frac{a}{b+c+d}+\frac{b}{c+d+a}+\frac{c}{d+a+b}+\frac{d}{a+b+c}\)
Giải:
Có: \(\frac{1}{a+b+c}+\frac{1}{b+c+d}+\frac{1}{c+d+a}+\frac{1}{d+a+b}=\frac{1}{40}\)
=> \(\frac{1}{2000-d}+\frac{1}{2000-a}+\frac{1}{2000-b}+\frac{1}{2000-c}=\frac{1}{40}\)
<=> \(\frac{2000}{2000-d}+\frac{2000}{2000-a}+\frac{2000}{2000-b}+\frac{2000}{2000-c}=\frac{2000}{40}\)
<=> \(1+\frac{d}{2000-d}+1+\frac{a}{2000-a}+1+\frac{b}{2000-b}+1+\frac{c}{2000-c}=50\)
<=> \(\frac{d}{a+b+c}+\frac{a}{b+c+d}+\frac{b}{a+c+d}+\frac{c}{a+b+d}=46\)
=> \(S=46\)
cho a+b+c+d=4000 và 1/a+b+c + 1/b+c+d+a +1/c+d+a + 1/d+a+b=1/40 .Tính gt của S=a/b+c+d +b/c+d+a +c/d+a+b +d/a+b+c
Ta có S = \(\frac{a}{b+c+d}+\frac{b}{c+d+a}+\frac{c}{d+a+b}+\frac{d}{a+b+c}\)
=> S + 4 = \(\left(\frac{a}{b+c+d}+1\right)+\left(\frac{b}{c+d+a}+1\right)+\left(\frac{c}{d+a+b}+1\right)+\left(\frac{d}{a+b+c}+1\right)\)
= \(\frac{a+b+c+d}{b+c+d}+\frac{a+b+c+d}{c+d+a}+\frac{a+b+c+d}{d+a+b}+\frac{a+b+c+d}{a+b+c}\)
\(=\left(a+b+c+d\right)\left(\frac{1}{b+c+d}+\frac{1}{c+d+a}+\frac{1}{d+a+b}+\frac{1}{a+b+c}\right)\)
\(=4000.\frac{1}{40}=100\)
=> S = 100 - 4 = 96
1) Tim tap xac dinh D cua ham so y = \(\sqrt{6-x}+\dfrac{2x+1}{1+\sqrt{x-1}}\)
A. D = R B. D = ( -∞; 6] C. D = (1; +∞ ) D. [1;6]
Lời giải:ĐKXĐ: \(\left\{\begin{matrix} 6-x\geq 0\\ x-1\geq 0\\ 1+\sqrt{x-1}\neq 0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x\leq 6\\ x\geq 1\end{matrix}\right.\) hay $x\in [1;6]$
Đáp án D
Đúng 0
Bình luận (0)
Cho hai đường thẳng d, d và M(2; -1; 0)d:
x
3
+
t
y
1
-
t
z
2
t...
Đọc tiếp
Cho hai đường thẳng d, d' và M(2; -1; 0)
d: x = 3 + t y = 1 - t z = 2 t , d': x = 1 + t ' y = 2 t ' z = - 1 + t '
Chứng minh rằng d và d' chéo nhau.
Ta chứng minh được d không song song với d' vì chúng có các vectơ chỉ phương không cùng phương.
Giải hệ phương trình
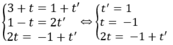
⇒ hệ phương trình vô nghiệm
Do đó d và d' chéo nhau.
Đúng 0
Bình luận (0)
Cho a+b+c+d=2000 và \(\dfrac{1}{a+b+c}+\dfrac{1}{b+c+d}+\dfrac{1}{c+d+a}+\dfrac{1}{d+a+b}=\dfrac{1}{40}\)
Tính S=\(\dfrac{a}{b+c+d}+\dfrac{b}{c+d+a}+\dfrac{c}{d+a+b}+\dfrac{d}{a+b+c}\)
cho a,b,c,d thỏa mãn a+b+c-5d/d=b+c+d-5a/a=c+d+a-5b/b=d+a+b-5c/c. tính giá trị của P=(1+b+c/a)(1+c+d/b)(1+d+a/c)(1+a+b/d)
a+b+c-2d/a=b+d+a-2c/b=b+d+c-2a/c=a+c+d-2b/d tính M=(1+a/b)(1+b/c)(1+c/d)(1+d/a)
\(\frac{a+b+c-2d}{a}=\frac{b+d+a-2c}{b}=\frac{b+d+c-2a}{c}=\frac{a+c+d-2b}{d}\)
\(=\frac{\left(a+b+c-2d\right)+\left(b+d+a-2c\right)+\left(b+d+c-2a\right)+\left(a+c+d-2b\right)}{a+b+c+d}\)
\(=\frac{a+b+c+d}{a+b+c+d}=1\)
\(\Leftrightarrow a=b=c=d\).
\(M=\left(1+\frac{a}{b}\right)\left(1+\frac{b}{c}\right)\left(1+\frac{c}{d}\right)\left(1+\frac{d}{a}\right)=2^4=16\)
Cho \(\dfrac{a+b+c-d}{d}\)=\(\dfrac{b+c+d-a}{a}\)=\(\dfrac{c+d+a-b}{b}\)=\(\dfrac{d+a+b-c}{c}\), (a+b+c+d) khác 0
tính giá trị của biểu thức: P=(1+\(\dfrac{b+c}{a}\))(1+\(\dfrac{c+d}{b}\))(1+\(\dfrac{d+a}{c}\))(1+\(\dfrac{a+b}{d}\))
Lời giải:
Áp dụng TCDTSBN:
$\frac{a+b+c-d}{d}=\frac{b+c+d-a}{a}=\frac{c+d+a-b}{b}=\frac{d+a+b-c}{c}$
$=\frac{a+b+c-d+b+c+d-a+c+d+a-b+d+a+b-c}{d+a+b+c}$
$=\frac{2(a+b+c+d)}{a+b+c+d}=2$
$\Rightarrow a+b+c-d=2d; b+c+d-a=2a; c+d+a-b=2b; d+a+b-c=2c$
$\Rightarrow a+b+c=3d; b+c+d=3a; c+d+a=3b; d+a+b=3c$
Khi đó:
\(P=\frac{a+b+c}{a}.\frac{b+c+d}{b}.\frac{c+d+a}{c}.\frac{a+b+d}{d}\\ =\frac{3d}{a}.\frac{3a}{b}.\frac{3b}{c}.\frac{3c}{d}=81\)
Đúng 1
Bình luận (0)
1. Cho d : y = (m2 + 2m)x + m + 1
Tìm m để :
a, d // d1 : y = (m + 6)x - 2
b, d ┸ d2 : y = -1/3x - 3
c, d ≡ d3 : y = -m2x + 1
2. Tìm d // d1 : y = -1/2x +1 và d đi qua giao điểm của d1 = 4x - 3 và d2 : y = -x +1
a: Để (d)//d1 thì \(\left\{{}\begin{matrix}m^2+m-6=0\\m+1\ne-2\end{matrix}\right.\Leftrightarrow m=2\)
Đúng 0
Bình luận (0)
Cho biểu thức
D = ( √a +1 /√a -1 - √a -1/√a+1 - 8√a/a-1 ) : ( √a-a-3/a -1 - 1/√a -1 )
a, Rút gọn D
b, tính giá trị của D khi a = 24 - 8√5
c, Tìm a để D = -1
d, Tìm a để D < √a + 3

























