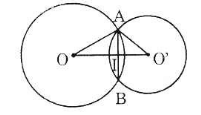
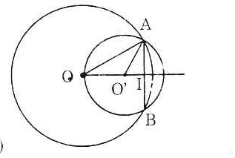
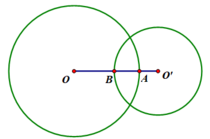
Cho hai đường tròn (O) và (O’) cắt nhau tại A và B như hình bên. Biết OA = 15cm, O’A = 13cm, AB = 24cm. Tính độ dài OO’.

Những câu hỏi liên quan
Cho hai đường tròn (O) và (O') cắt nhau tại A và B như hình 77. Biết OA = 15cm, O'A = 13 cm, AB = 24cm. Tính độ dài OO' ?

cho hai đường tròn (O;20cm) và (O';15cm) cắt nhau tại A, B. Tính đoạn nối tâm OO' biết rằng AB=24cm. ( Xét hai trường hợp; O và O' nằm khác phía đối với AB; O và O' nằm cùng phía đối với AB)
- Trường hợp 1: O và O' nằm khác phía đối với AB
Gọi I là giao điểm của OO' và AB. Theo tính chất đường nối tâm ta có
\(AB\perp OO'\) ; AI = IB = 12
Áp dụng định lí Pitago , ta được :
\(OI=\sqrt{OA^2-AI^2}=\sqrt{20^2-12^2}=\sqrt{256}=16\left(cm\right)\)
\(IO'=\sqrt{O'A^2-AI^2}=\sqrt{15^2-12^2}=\sqrt{81}=9\left(cm\right)\)
Vậy OO' = OI + IO' = 16 + 9 = 25 ( cm )
- Trường hợp 2: O và O' nằm cùng phía đối với AB
Như TH1 , ta lại có :
\(OI=\sqrt{OA^2-AI^2}=16\left(cm\right)\)
\(O'I=\sqrt{O'A^2-AI^2}=9\left(cm\right)\)
Vậy OO' = OI – O'I = 16 – 9 = 7 ( cm )
Cho hai đường tròn (O;20cm) và (O';15cm) cắt nhau tại A và B. Tính đoạn nối tâm OO'; biết rằng AB = 24cm (Xét hai trường hợp : O và O' nằm khác phía đối với AB; O và O' nằm cùng phía đối với AB)
a) Trường hợp O và O’ nằm khác phía đối với AB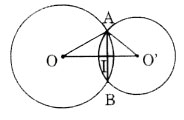
Ta có: AI =1/2 AB = 12
OI2 = OA2 – AI2
=400-144 =256
⇒ OI =16
O’I2 = O’A2 – AI2 =255 -144 =81
⇒ O’I = 9
Ta có: OO’ = OI + OI’ = 16 + 9 =25 (cm).
b) Trường hợp O và O’ nằm cùng phía đối với AB.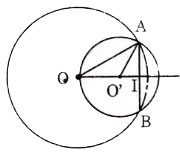
Ta có: OI2 = OA2 – AI2 = 256
⇒ OI =16
Tương tự O’I= 9
Do đó: OO’= OI – O’I =16 – 9= 7(cm)
Đúng 0
Bình luận (0)
Cho 2 đường tròn (O; 4cm) và (O’; 2cm) sao cho khoảng cách giữa hai tâm O và O’ là 5cm. Đường tròn (O; 4cm) cắt đoạn OO’ tại điểm A và đường tròn (O’; 2cm) cắt đoạn OO’ tại điểm B. Tính O’A, BO, AB?
Cho hai đường tròn (O;15cm) và (I;13cm) cắt nahu tại A và B.Biết khoảng cách giữa hai tâm là 14cm.Độ dài dây cung AB là
A.12cm B.24cm C.14cm D.28cm
Cho hai đường tròn (O;13cm) và (O'10cm) cắt nhau tại hai điểm phân biệt A,B. Đoạn OO' cắt (O);(O') lần lượt tại E và F . Biết EF=3cm , độ dài OO' là A.20cm B.18cm C.19cm D.16cm
Giúp mk với ak
độ dài \(OO'=20cm\)
Ta có: \(EF=OE+O'F-OO'\Rightarrow3=13+10-OO'\)
\(\Rightarrow OO'=20\)
Đúng 3
Bình luận (0)
Cho đoạn thẳng OO’ và điểm A nằm giữa hai điểm O và O’. vẽ đường tròn (O; OA) và đường tròn (O’; O’A). Qua A vẽ đường thẳng cắt (O) tại B và cắt (O’) tại C.
a)Chứng minh(O) và (O’) tiếp xúc với nhau.
b)Vẽ đường kính BD của (O) và đường kính CE của (O’). Chứng minh D, A, E thẳng hàng.
Cho 2 đường tròn (O; 20 cm) và (O'; 15 cm) cắt nhau tại hai điểm M và N . Gọi I là giao điểm của MN và OO'
a, CM OO' vuông góc với MN
b, Cho MN = 24cm , Tính độ dài đth MI
c, Tính độ dài đoạn OO' . CM O'M là tiếp tuyến của đường tròn (O)
Cho đường tròn (O; 15cm ). Dây BC= 24cm. Các tiếp tuyến của đường tròn (O) tại B và C cắt nhau tại A a/ tính khoảng cách từ tâm đến dây BC b/ chứng minh ba điểm O;A;H thẳng hàng c/ tính độ dài AB và AC
a: ΔOBC cân tại O
mà OH là đường cao
nên H là trung điểm của BC
=>HB=HC=12cm
=>\(OH=\sqrt{15^2-12^2}=9\left(cm\right)\)
b: Xét (O) có
AB,AC là tiếp tuyến
nên AB=AC
=>A nằm trên trung trực của BC
mà OH là trung trực của BC
nên O,H,A thẳng hàng
c: OA=OB^2/OH=15^2/9=25cm
=>AB=AC=20cm
Đúng 0
Bình luận (0)