Vẽ một lục giác đều ABCDEF có tất cả các đỉnh nằm trên đường tròn (O)

Những câu hỏi liên quan
a) Vẽ đường tròn tâm O bán kính R = 2cm.
b) Vẽ một lục giác đều ABCDEF có tất cả các đỉnh nằm trên đường tròn (O).
c) Vì sao tâm O cách đều các cạnh của lục giác đều ? Gọi khoảng cách này là r.
d) Vẽ đường tròn (O; r).
a)
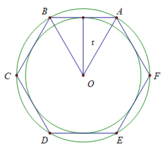
b) Cách vẽ lục giác đều có tất cả các đỉnh nằm trên đường tròn (O)
Vẽ các dây cung AB = BC = CD = DE = EF = FA = R = 2 cm
(Ta đã nêu được cách chia đường tròn thành sáu cung bằng nhau tại bài tập 10 SGK trang 71)
c) Vì các dây cung AB = BC = CD = DE = EF = FA bằng nhau nên khoảng cách từ O đến các dây là bằng nhau ( định lý liên hệ giữa dây cung và khoảng cách từ tâm đến dây)
Đúng 0
Bình luận (0)
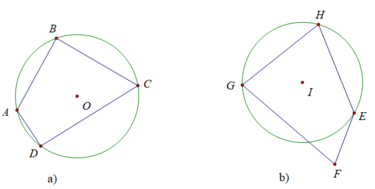
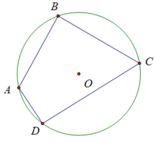
a) Vẽ một đường tròn tâm O rồi vẽ một tứ giác có tất cả các đỉnh nằm trên đường tròn đó.
b) Vẽ một đường tròn tâm I rồi vẽ một tứ giác có ba đỉnh nằm trên đường tròn đó còn đỉnh thức tư thì không.
Vẽ một đường tròn tâm O rồi vẽ một tứ giác có tất cả các đỉnh nằm trên đường tròn đó.
Đề bài
a) Vẽ đường tròn tâm O bán kính R = 2cm.
b) Vẽ một lục giác đều ABCDEF có tất cả các đỉnh nằm trên đường tròn (O).
c) Vì sao tâm O cách đều các cạnh của lục giác đều ? Gọi khoảng cách này là r.
d) Vẽ đường tròn (O; r).
Dễ. Bạn chỉ cần vễ bằng ê-kê là xong
cái này toán lớp 9 của cj mk đó giải giúp cj mk ik , ko biết thì mới phải hỏi mn mà ...!
Sorry chị nha , em mới học lớp 4 nên ko giải đc
Xem thêm câu trả lời
Cho lục giác lồi ABCDEF có AB // DE, BC // EF, AF // CD và AD = BE = CF. Chứng minh lục giác có 6 đỉnh cùng nằm trên 1 đường tròn.
Một hình lục giác đều ABCDEF (các đỉnh lấy theo thứ tự đó và ngược chiều quay của kim đồng hồ) nội tiếp trong đường tròn tâm O. Tính số bằng rađian của các cung lượng giác: cung AB, AC, AD, AE, AF.
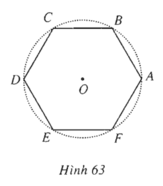
Sđ cung AB = π/3 + k2π, k ∈ Z
Sđ cung AC = 2π/3 + k2π, k ∈ Z
Sđ cung AD = π + k2π, k ∈ Z
Sđ cung AE = 4π/3 + k2π, k ∈ Z
Sđ cung AF = 5π/3 + k2π, k ∈ Z
Đúng 0
Bình luận (0)
Cho một đa giác đều 18 đỉnh nội tiếp trong một đường tròn tâm O. Gọi X là tập hợp tất cả các tam giác có các đỉnh là các đỉnh của đa giác trên. Tính xác suất P để chọn được một tam giác từ tập X là tam giác cân nhưng không phải tam giác đều
Cho ABCDEF là lục giác lồi nội tiếp đường tròn bán kính R có các cạnh AB=CA=EF=R. Chứng minh rằng trung điểm 3 cạnh BC, DE, FA là đỉnh của một tam giác đều.
Ta cần chứng minh tam giác MNP là tam giác cân và có một góc bằng \(\frac{\Pi}{3}\)
Giả sử lục giacs có hướng âm, kí hiệu \(f\) là phép quay vec tơ theo góc \(-\frac{\Pi}{3}\) và M, N. P theo thứ tự là trung điểm FA, BC, DE
Khi đó AB=BO, CD=DO=OC, EF=FO=OE nên các tam giác ABO, CDO, EFO đều và có hướng âm
Suy ra \(f\left(\overrightarrow{AB}\right)=\overrightarrow{AO}\), \(f\left(\overrightarrow{OC}\right)=\overrightarrow{OD}\), \(f\left(\overrightarrow{FO}\right)=\overrightarrow{FE}\)
Từ đó ta có :
\(f\left(\overrightarrow{MN}\right)=f\left(\frac{1}{2}\left(\overrightarrow{AB}+\overrightarrow{FC}\right)\right)=\frac{1}{2}\left(f\left(\overrightarrow{AB}\right)+f\left(\overrightarrow{FC}\right)\right)\)
\(=\frac{1}{2}\left(\overrightarrow{AO}\right)+\overrightarrow{OD}+\overrightarrow{FE}=\frac{1}{2}\left(\overrightarrow{AD}+\overrightarrow{FE}\right)\)
\(=\overrightarrow{MP}\)
Suy ra tam giác MNP cân và có góc PMN = \(\frac{\Pi}{3}\) => Điều phải chứng minh
Đúng 0
Bình luận (0)
Cho hình lục giác đều ABCDEF có cạnh bằng 2 (tham khảo hình vẽ). Quay lục giác xung quanh đường chéo AD ta được một khối tròn xoay. Thể tích khối tròn xoay đó là A.
V
8
π
B.
V
7
π
C.
V
8
π
3
3...
Đọc tiếp
Cho hình lục giác đều ABCDEF có cạnh bằng 2 (tham khảo hình vẽ). Quay lục giác xung quanh đường chéo AD ta được một khối tròn xoay. Thể tích khối tròn xoay đó là
A. V = 8 π
B. V = 7 π
C. V = 8 π 3 3
D. V = 7 π 3 3
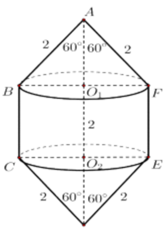
Gọi thể tích của khối tròn xoay là V, thể tích
khối nón là V 1 và thể tích của khối trụ là V 2 .
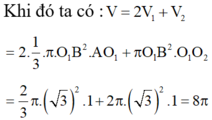
Đúng 0
Bình luận (0)