Cho a và b là các số nguyên dương lim x → 0 a a x - 1 sin b x = 5 3 Tích có thể nhận giá trị bằng số nào trong các số dưới đây?
A. 15.
B. 60.
C. 240.
D. Cả ba đáp án trên.
Tổng giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số f(x) = (x-6) x 2 + 4 trên đoạn [0;3] có dạng a - b c với a là số nguyên và b, c là các số nguyên dương. Tính S = a + b + c.
A. 4
B. -2
C. -22
D. 5
Chọn A
Hàm số f(x) = (x-6) x 2 + 4 xác định và liên tục trên đoạn [0;3].
![]()
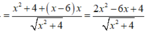

![]()
Suy ra ![]()
![]()
![]() với a là số nguyên và b, c là các số nguyên dương nên
với a là số nguyên và b, c là các số nguyên dương nên
a = - 12, b = 3, c = 13. Do đó: S = a + b + c = 4.
Biết lim x → 8 x + 1 - x + 19 3 x + 8 4 - 2 = a b trong đó a/b là phân số tối giản, a và b là các số nguyên dương. Tổng a + b bằng
A. 137.
B. 138.
C. 139.
D. 140.
Chọn C.
Đặt t = x - 8. Suy ra x = t + 8. ![]() và
và
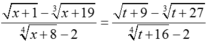
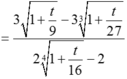
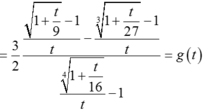
Do đó 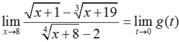 . Áp dụng ví dụ 13. Ta có:
. Áp dụng ví dụ 13. Ta có:
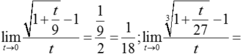
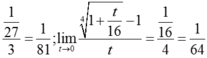
Vậy 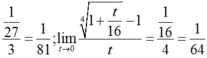 .
.
Do đó 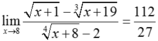 .
.
Vậy a =112; b = 27 và a + b = 139.
Cho số tự nhiên B=axby, trong đó a, b là các số nguyên dương khác nhau và x, y là các số tự nhiên khác 0. Biết B2 có 15 ước. Vậy B3 có tất cả bao nhiêu ước?
Cho a, b, c, x, y, z là các số nguyên dương và 3 số a, b, c khác 1 thỏa mãn: \(a^x=bc;b^y=ca;c^a=ab\) CMR : \(x+y+z+2=xyz\)
somebody HELP !!!!
Tiểu_Thư_cute
Ta có :
a^xyz=(a^x)^yz=(bc)^yz
=b^yz.c^yz
=(b^y)^z.(c^z)^y
=(ca)^z.(ab)^y
=c^z.a^z.a^y.b^y
=(bc).a^z.a^y.(ca)
=a^2.a^y.a^z.(bc)
=a^2.a^y.a^z.a^x
=a^(x+y+z+2)
=>xyz=x+y+z+2
Tìm tất cả các số nguyên dương x,y sao cho các số x² +3y và y² +3x đêug là số chính phương
Xét xem các số a và b có thể là số vô tỉ hay ko nếu :
a) ab và a/b là các số hữu tỉ
b) a + b và a/b là các số hữu tỉ (a + b khác 0)
c) a + b và a^2 b^2 là các số hữu tỉ ( a + b khác 0)
Ai làm đc mình cho 3 like
Cho 3 **** kiểu gì nào?
a) a,b có thể là số vô tỉ. Ví dụ \(a=b=\sqrt{2}\) là vô tỉ mà ab và a/b đều hữu tỉ.
b) Trong trường hợp này \(a,b\) không là số vô tỉ (tức cả a,b đều là số hữu tỉ). Thực vậy theo giả thiết \(a=bt\), với \(t\) là số hữu tỉ khác \(-1\). Khi đó \(a+b=b\left(1+t\right)=s\) là số hữu tỉ, suy ra \(b=\frac{s}{1+t}\) là số hữu tỉ. Vì vậy \(a=bt\) cũng hữu tỉ.
c) Trong trường hợp này \(a,b\) có thể kaf số vô tỉ. Ví dụ ta lấy \(a=1-\sqrt{3},b=3+\sqrt{3}\to a,b\) vô tỉ nhưng \(a+b=4\) là số hữu tỉ và \(a^2b^2=\left(ab\right)^2=12\) cũng là số hữu tỉ.
Cho x, y là các số thực dương và x ≠ y . Biểu thức A = x 2 x + y 2 x 2 - 4 1 2 x xy 2 x bằng
A. y 2 x - x 2 x
B. x 2 x - y 2 x
C. x - y 2 x
D. x 2 x - y 2 x
Cho a và là 2 số nguyên dương thỏa mãn các tính chất sau:
a. (a+1) chia hết cho b
b. a=2b+5
c. a+7b là số nguyên tô
Hãy tìm a và b
Lời giải:
a+1\vdots b$
$\Rightarrow 2b+5+1\vdots b$
$\Rightarrow 2b+6\vdots b$
$\Rightarrow 6\vdots b\Rightarrow b\in \left\{1; 2; 3; 6\right\}$
Nếu $b=1$ thì $a=7$. Khi đó $a+7b=14$ không là snt (loại)
Nếu $b=2$ thì $a=9$. Khi đó $a+7b = 23$ là snt (thỏa mãn)
Nếu $b=3$ thì $a=11$. Khi đó $a+7b=32$ không là snt (loại)
Nếu $b=6$ thì $a=17$. Khi đó $a+7b = 59$ là snt (thỏa mãn)
Vậy.........
chuyên đề phân tích đa thức thành nhân tử
1)tách 1 hạng tử hành nhiều hạng tử
định lý bổ sung;
+đa thức f(x)có nghiệm hữu tỉ thì có dạng p/q trong đó p là ước của hệ số tự do ,q là ước dương của hệ số cao nhất
+nếu f(x) có tổng các hệ số bằng 0 thì f(x) có 1 nhân tử là x-1
+nếu f(x) có tổng các hệ số của các hạng tử bậc chẵn bằng tổng các hệ số của các hạng tử bậc lẻ thì f9x) có 1 nhân tử là x+1
+nếu a là nghiệm nguyên của f(x) và f(1),f(-1) khác 0 thì \(\frac{f\left(1\right)}{a-1}\) và \(\frac{f\left(-1\right)}{a+1}\)đều là số nguyên
cho tớ mỗi dấu cộng là 1 ví dụ nhé .tớ chưa hiểu lém