Cho CSN (un) thỏa:. u 1 + u 2 + u 3 + u 4 + u 5 = 11 u 1 + u 5 = 82 11 Tính tổng S2011
A. q = 1 3 ; S 2011 = 243 22 ( 1 - 1 3 2011 )
B. q = 3 ; S 2011 = 1 22 ( 3 2011 - 1 )
C. Cả A, B đúng
D. Cả A, B sai
Cho CSN (un) thỏa: u 1 + u 2 + u 3 + u 4 + u 5 = 11 u 1 + u 5 = 82 11 Trên khoảng (1/2; 1) có bao nhiêu số hạng của cấp số.
A. 1
B. 2
C. 3
D. 4
Chọn B.
Với q = 3 ta có:  nên có một số hạng của dãy
nên có một số hạng của dãy
Với q = 1/3 ta có:  nên có một số hạng của dãy.
nên có một số hạng của dãy.
1. cho dãy (Un) =2.3n . CM dãy lập thành cấp số nhân. Tìm u1 và q.
2. Cho CSN (Un) #0. Khi nào thì Un tạo thành CSC. Tìm q và d.
Cho CSN (un) thỏa: u 1 + u 2 + u 3 + u 4 + u 5 = 11 u 1 + u 5 = 82 11 Tìm công bội và số hạng tổng quát của cấp số
A. q = 3 ; u n = 3 n - 1 11
B. q = 1 3 ; u n = 81 11 . 1 3 n - 1
C. Cả A, B đúng
D. Cả A, B
Chọn C.
Gọi q là công bội của cấp số. Khi đó ta có:
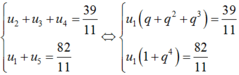
Suy ra: 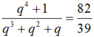 ⇔ 39q4 – 82q3 -82q2 -82q + 39 = 0
⇔ 39q4 – 82q3 -82q2 -82q + 39 = 0
⇔ (3q – 1)(q – 3)(13q2 + 16q + 13) = 0 ⇔ q = 1/3, q = 3
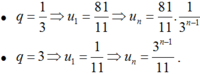
1) cho CSN (un) có u2.u3=27 ,u3+u5=90 thì q =?
2 ) cho CSN 9,3,1,.... thì q =?
2: q=1/3
1: =>u1*q*u1*q^2=27 và u1*q^2+u1*q^4=90
=>u1^2*q^3=27 và u1*q^2(1+q^2)=90
=>q/1+q^2=3/10 và u1^2*q^3=27
=>3q^2+3-10q=0 và u1^2*q^3=27
=>q=3 hoặc q=1/3
Cho CSN (Un) biết U1 = 1, U7= 729. Tìm q và số hạng thứ 8 của CSN.
\(u_7=u_1.q^6\Rightarrow q^6=729\Rightarrow q=\pm3\)
Với \(q=3\Rightarrow u_8=u_7.q=2187\)
Với \(q=-3\Rightarrow u_8=-3.729=-2187\)
1/ CSN un có u1=3, q=√2. Tính u3+u7+u11+...+u35
2/ CSN có u1=1,q=√3. Tính u12+u22+...+u202
3/ CSN hữu hạn có tổng bình phương tất cả số hạng bằng 484, u1=2,số hạng cuối =18. Tìm q
4/ 3 số x, 3,y theo thứ tự lập thành CSN thỏa x^4=y√3. Tìm x, y
\(u_3+u_7+...+u_{35}=u_1q^2+u_1q^6+...+u_1q^{34}\)
\(=u_1q^2\left(1+q^4+q^8+...+q^{32}\right)=u_1q^2.\frac{\left(q^4\right)^9-1}{q^4-1}=524286\)
2/ \(u_1^2+u_2^2+...+u_{20}^2=u_1^2+u_1^2q^2+u_1^2q^4+...+u_1^2q^{38}\)
\(=u_1^2\left(1+q^2+q^4+...+q^{38}\right)=u_1^2\frac{\left(q^2\right)^{20}-1}{q^2-1}=\frac{3^{20}-1}{2}\)
3/
\(u_1=2;u_n=18\)
\(u_1^2+u_2^2+...+u_n^2=484\)
\(\Leftrightarrow u_1^2+u_1^2q^2+...+u_1^2q^{2\left(n-1\right)}=484\)
\(\Leftrightarrow u_1^2\left(1+q^2+...+q^{2\left(n-1\right)}\right)=484\)
\(\Leftrightarrow1+q^2+...+q^{2\left(n-1\right)}=121\)
\(\Leftrightarrow\frac{q^{2n}-1}{q^2-1}=121\)
Mà \(u_n=u_1q^{n-1}\Rightarrow q^{n-1}=\frac{u_n}{u_1}=9\Rightarrow q^n=9q\Rightarrow q^{2n}=81q^2\)
\(\Rightarrow\frac{81q^2-1}{q^2-1}=121\Rightarrow81q^2-1=121q^2-121\)
\(\Rightarrow q^2=3\Rightarrow q=\pm\sqrt{3}\)
4/
Do 3 số đã cho lập thành CSN nên ta có:
\(xy=3^2=9\Rightarrow y=\frac{9}{x}\)
Mà \(x^4=y\sqrt{3}\)
\(\Rightarrow x^4=\frac{9\sqrt{3}}{x}\Rightarrow x^5=9\sqrt{3}=\sqrt{3}^5\)
\(\Rightarrow x=\sqrt{3}\)
\(\Rightarrow y=3\sqrt{3}\)
Cho dãy u(n) thỏa mãn log 3 u 1 2 - 3 log u 5 = log 3 u 2 + 9 - log u 1 6 và u n + 1 = u n + 3 u 1 > 0 với mọi n≥1 Đặt S n = u 1 + u 2 + . . . + u n Tìm giá trị nhỏ nhất của n để S n > 5 n 2 + 2018 2
A. 1647
B. 1650
C. 1648
D. 1165
Cho CSN (un) biết S2 = 4, S3 = 13. Tìm S5
Lời giải:
Gọi $d$ là công sai và số $S_1=n$. Ta có:
$S_2=S_1+d=n+d$
$S_3=S_2+d=S_1+2d=n+2d$
$\Rightarrow S_3-S_2=d$
Hay $9=d$. Khi đó:
$S_2=n+d\Rightarrow n=S_2-d=4-9=-5$
Khi đó:
$S_5=n+(5-1)d=-5+4.9=31$
Cho dãy (un) thỏa mãn: \(\left\{{}\begin{matrix}u_1=5\\u_{n+1}=\dfrac{u^{2022}_n+3.u_n+16}{u_n^{2021}-u_n+11}\end{matrix}\right.\), ∀nϵN*
CMR (un) tăng
Xét hàm số \(f\left(x\right)=\dfrac{x^{2022}+3x+16}{x^{2021}-x+11}\), ta cần cm
\(f\left(x\right)\ge x\) (*)
Thật vậy, (*) \(\Leftrightarrow x^{2022}+3x+16\ge x^{2022}-x^2+11x\)
\(\Leftrightarrow x^2-8x+16\ge0\)
\(\Leftrightarrow\left(x-4\right)^2\ge0\) (luôn đúng)
Vậy \(f\left(x\right)\ge x,\forall x\)
\(\Rightarrow u_{n+1}=f\left(u_n\right)\ge u_n\) nên \(\left(u_n\right)\) là dãy tăng.