Trong các dãy số sau, dãy số nào là một cấp số nhân?
A. 128 ; − 64 ; 32 ; − 16 ; 8 ; ...
B. 2 ; 2 ; 4 ; 4 2 ; ....
C. 5 ; 6 ; 7 ; 8 ; ...
D. 1 π ; 1 π 2 ; 1 π 4 ; 1 π 6 ; ⋯
Những câu hỏi liên quan
Trong các dãy số sau, dãy số nào là một cấp số nhân.
A. 1;-2;4;-8;-16;-32
B. 1;3;9;17;81;243
C. 2;4;6;8;12;16;32;63
D. 4;2;1;0,5;-0,25
Chọn B.
- Theo tính chất của cấp số nhân: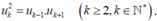 
+ Đáp án A: ( - 8 ) 2 ≠ - 4 . 16 nên A sai.
+ Đáp án C: 6 2 ≠ 4 . 8 nên C sai.
+ Đáp án D: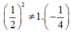 
nên D sai.
Đúng 0
Bình luận (0)
Trong các dãy số sau, dãy số nào là cấp số nhân? A.
u
n
5
n
+
3
,
n
≥
1
B.
u
n
4
+
3
n
,
n
≥
1
C.
u
1...
Đọc tiếp
Trong các dãy số sau, dãy số nào là cấp số nhân?
A. u n = 5 n + 3 , n ≥ 1
B. u n = 4 + 3 n , n ≥ 1
C. u 1 = 3 u n + 1 = 7 u n , n ≥ 1
D. u 1 = 2 u n + 1 = u 2 n , n ≥ 1
Trong các dãy số sau đây dãy số nào là cấp số nhân? A. Dãy số
u
n
, xác định bởi hệ :
u
1
1
u
n
u...
Đọc tiếp
Trong các dãy số sau đây dãy số nào là cấp số nhân?
A. Dãy số u n , xác định bởi hệ : u 1 = 1 u n = u n − 1 + 2 n ∈ ℕ * : n ≥ 2
B. Dãy số các số tự nhiên 1; 2; 3....
C. Dãy số u n , xác định bởi công thức u n = 3 n + 1 v ớ i n ∈ ℕ *
D. Dãy số − 2 ; 2 ; − 2 ; 2 ; ... ; − 2 ; 2 ; − 2 ; 2 ; ...
Trong các dãy số sau đây dãy số nào là cấp số nhân? A. Dãy số -2,2,-2,2,...,-2,2,-2,2... B. Dãy số các số tự nhiên 1, 2, 3,... C. Dãy số
u
n
, xác định bởi công thức:
u
n
3
n
+
1
v
ớ
i
n
∈
N
*...
Đọc tiếp
Trong các dãy số sau đây dãy số nào là cấp số nhân?
A. Dãy số -2,2,-2,2,...,-2,2,-2,2...
B. Dãy số các số tự nhiên 1, 2, 3,...
C. Dãy số u n , xác định bởi công thức:
u n = 3 n + 1 v ớ i n ∈ N * với n ∈ N *
D. Dãy số u n , xác định bởi hệ:
u 1 = 1 u n = u n - 1 + 2 ( n ∈ N * : n ≥ 2 )
Trong các dãy số
(
u
n
)
sau, dãy nào là cấp số nhân? A.
u
n
n
2
+
n
+
1
B.
u
n
n
+
2
.3
n
C.
u...
Đọc tiếp
Trong các dãy số ( u n ) sau, dãy nào là cấp số nhân?
A. u n = n 2 + n + 1
B. u n = n + 2 .3 n
C. u 1 = 2 u n + 1 = 6 u n , ∀ n ∈ ℕ * .
D. u n = − 4 2 n + 1
Kiểm tra đáp án
A. u n + 1 u n = ( n + 1 ) 2 + 3 ( n + 1 ) + 3 n 2 + n + 1 = n 2 + 5 n + 7 n 2 + n + 1 , ∀ n ∈ ℕ * , không phải là hằng số.
Vậy ( u n ) không phải là cấp số nhân .
B. u n + 1 u n = n + 3 .3 n + 1 n + 2 .3 n = 3 n + 3 n + 2 , ∀ n ∈ ℕ * , không phải là hằng số.
Vậy ( u n ) không phải là cấp số nhân .
C. Từ công thức truy hồi của dãy số, suy ra u 1 = 2 ; u 2 = 3 ; u 3 = 2 ; u 4 = 3 ; ...
Vì u 3 u 2 ≠ u 2 u 1 nên ( u n ) không phải là cấp số nhân .
D. u n + 1 u n = − 4 2 n + 1 + 1 − 4 2 n + 1 = − 4 2 n + 2 + 1 − 4 2 n + 1 = ( − 4 ) 2 = 16 , ∀ n ∈ ℕ * .
Vậy ( u n ) là một cấp số nhân.
Chọn đáp án D
Đúng 0
Bình luận (0)
Trong các dãy số
u
n
sau đây, dãy số nào là cấp số nhân ? A.
u
n
3
n
B.
u
n
2...
Đọc tiếp
Trong các dãy số u n sau đây, dãy số nào là cấp số nhân ?
A. u n = 3 n
B. u n = 2 n
C. u n = 1 n
D. u n = 2 n + 1
Chọn B
Ta thấy, với ∀ n ≥ 2 , n ∈ ℕ dãy số u n = 2 n có tính chất:
u n u n - 1 = 2 n 2 n - 1 = 2 nên là cấp số nhân với công bội q = 2 , u 1 = 2
Đúng 0
Bình luận (0)
Trong các dãy số
u
n
sau đây, dãy số nào là cấp số nhân? A.
u
n
3
n
B.
u
n
2
n
C.
u
n
1
n
D.
u...
Đọc tiếp
Trong các dãy số u n sau đây, dãy số nào là cấp số nhân?
A. u n = 3 n
B. u n = 2 n
C. u n = 1 n
D. u n = 2 n + 1
Trong các dãy số cho dưới đây, dãy số nào không phải là một cấp số nhân lùi vô hạn? A.
2
3
,
4
9
,
8
27
,
.
.
....
Đọc tiếp
Trong các dãy số cho dưới đây, dãy số nào không phải là một cấp số nhân lùi vô hạn?
A. 2 3 , 4 9 , 8 27 , . . . , 2 3 n , . . .
B. 1 3 , 1 9 , 1 27 , . . . , 1 3 n , . . .
C. 3 2 , 9 4 , 27 8 , . . . , 3 2 n , . . .
D. 1 , - 1 2 , 1 4 , - 1 8 , . . . , - 1 2 n - 1 , . . .
Chọn đáp án C vì dãy ở đây là một CSN có công bội q = 3 2 > 1 ,
nên dãy 3 2 , 9 4 , 27 8 , . . . , 3 2 n , . . . không phải là dãy lùi vô hạn.
Chọn C
Đúng 0
Bình luận (0)
Trong các dãy số cho dưới đây, dãy số nào không phải là một cấp số nhân lùi vô hạn? A.
2
3
,
4
9
,
8
27
,
.
.
.
,
2
3
n
,
....
Đọc tiếp
Trong các dãy số cho dưới đây, dãy số nào không phải là một cấp số nhân lùi vô hạn?
A. 2 3 , 4 9 , 8 27 , . . . , 2 3 n , . . .
B. 1 3 , 1 9 , 1 27 , . . . , 1 3 n , . .
C. 3 2 , 9 4 , 27 8 , . . . , 3 2 n , . . .
D. 1 , - 1 2 , 1 4 , - 1 8 , 1 16 , . . . , - 1 2 n - 1 , . . .
Đáp án C
Chọn đáp án C vì dãy ở đây là một CSN có công bội q = 3 2 > 1 , nên dãy 3 2 , 9 4 , 27 8 , . . . , 3 2 n không phải là dãy lùi vô hạn
Đúng 0
Bình luận (0)