c, giao điểm 2 đường phân giác

chúc bn hok tốt!

đúng thì k cho mk nha!

mk ghi nhầm, 2 sửa thành 3 nha

giao điểm của ba đường phân giác

Chọn (D) Ba đường cao.

câu a: ba đường trung tuyến nha bn !

Ba đường trung tuyến

ba đường trung tuyến nhé bạn

Chọn C

A. Phân giác.

A

A

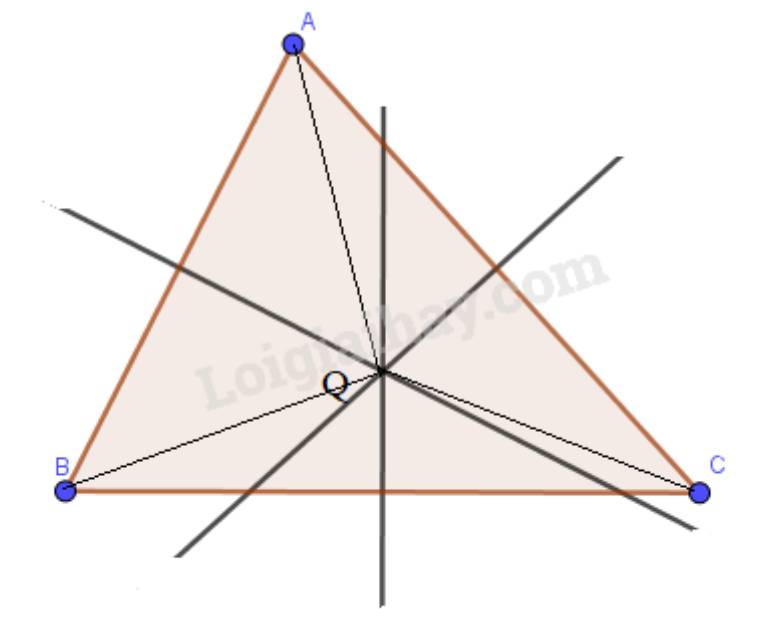
Vì Q cách đều 3 đỉnh của tam giác ABC nên QA=QB=QC

Vì QA=QB nên Q nằm trên đường trung trực của đoạn thẳng AB (tính chất đường trung trực của đoạn thẳng).

Vì QA=QC nên Q nằm trên đường trung trực của đoạn thẳng AC (tính chất đường trung trực của đoạn thẳng).

Vì QB=QC nên Q nằm trên đường trung trực của đoạn thẳng BC (tính chất đường trung trực của đoạn thẳng).

Vậy Q là giao điểm của 3 đường trung trực của tam giác ABC.

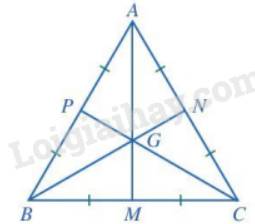
Gọi M, N, P lần lượt là các trung điểm của các đoạn thẳng BC, AC, AB.

Ta có: G là giao điểm của ba đường trung tuyến trong tam giác ABC.

Mà G cũng là giao điểm của ba đường trung trực trong tam giác ABC nên AM, BN, CP là các đường trung trực của tam giác ABC hay \(AM \bot BC;BN \bot AC;CP \bot AB\).

Xét tam giác ABM và tam giác ACM có:

     AM chung;

     \(\widehat {AMB} = \widehat {AMC} (= 90^\circ \))(vì \(AM \bot BC\));

     BM = MC (M là trung điểm của BC).

Vậy \(\Delta ABM = \Delta ACM\)(c.g.c). Suy ra: AB = AC ( 2 cạnh tương ứng). (1)

Tương tự ta có:

     \(\Delta BNA = \Delta BNC\)(c.g.c). Suy ra: AB = BC( 2 cạnh tương ứng). (2)

Từ (1) và (2) suy ra: AB = BC = AC.

Vậy tam giác ABC đều.

a)

Ta có:

     G là trọng tâm của tam giác ABC (giao điểm của ba đường trung tuyến);

     H là trực tâm của tam giác ABC (giao điểm của ba đường cao);

     I là giao điểm của ba đường phân giác của tam giác ABC;

     O là giao điểm của ba đường trung trực của tam giác ABC (Đường trung trực đi qua trung điểm của cạnh và vuông góc với cạnh tại trung điểm đó).

Mà tam giác ABC đều nên trong tam giác ABC đường trung tuyến đồng thời là đường cao và là đường phân giác.

Vậy bốn điểm G, H, I, O trùng nhau hay nếu tam giác ABC đều thì bốn điểm G, H, I, O trùng nhau.

b) 

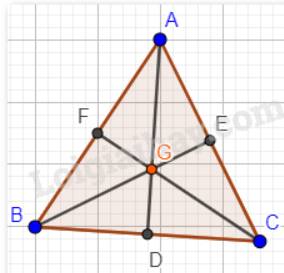
Giả sử trong tam giác ABC có hai điểm trùng nhau là H (trực tâm của tam giác) và I (giao của ba đường phân giác).

Hay AD, BE, CF vừa là đường cao, vừa là đường phân giác của tam giác ABC.

Xét tam giác ADB và tam giác ADC có:

\(\widehat {BAD} = \widehat {CAD}\) ( vì AD là tia phân giác của góc BAC)

AD chung;

\(\widehat {ADB} = \widehat {ADC}(=90^0)\) (vì \(AD \bot BC\));

Vậy \(\Delta ADB = \Delta ADC\)(g.c.g). Suy ra: AB = AC( 2 cạnh tương ứng). (1)

Tương tự ta có: \(\Delta AEB = \Delta CEB\)(c.g.c). Suy ra: AB = BC ( 2 cạnh tương ứng). (2)

Từ (1) và (2) suy ra: AB = BC = AC.

Vậy tam giác ABC đều hay nếu tam giác ABC có hai điểm trong bốn điểm G, H, I, O trùng nhau thì tam giác ABC là tam giác đều.