Cho hình chóp S . A B C D có đáy ABCD là hình vuông tâm O cạnh a. Cạnh bên S A = a 2 và vuông góc với đáy (ABCD). Khoảng cách từ điểm B đến mặt phẳng (SCD) bằng
A. a
B. a 3
C. a 3 2
D. a 6 3
Bài 10. Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 2a, cạnh bên bằng a * sqrt(3) . O là tâm hình vuông 1/ Chứng minh :a) (SAC) I (ABCD) b) (SAC) (SBD). 2 / a ) Tính d(S; (ABCD)) b) Tính d(O; (SCD)) 3/ Tính góc giữa:a) SC và (ABCD); b) (SAB) và (ABCD).
a: SO vuông góc (ABCD)
=>(SAC) vuông góc (ABCD)
b: AC vuông góc BD
BD vuông góc SO
=>BD vuông góc (SAC)
=>(SBD) vuông goc (SAC)
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O, cạnh a. Cạnh bên \(SA=a\sqrt{3}\) và vuông góc với đáy (ABCD). Tính khoảng cách d từ điểm A đến mặt phẳng (SBD).
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp BD\\BD\perp AC\end{matrix}\right.\) \(\Rightarrow BD\perp\left(SAC\right)\)
Từ A kẻ \(AH\perp SO\Rightarrow AH\perp\left(SBD\right)\)
\(\Rightarrow AH=d\left(A;\left(SBD\right)\right)\)
\(AC=a\sqrt{2}\Rightarrow AO=\dfrac{1}{2}AC=\dfrac{a\sqrt{2}}{2}\)
Hệ thức lượng: \(\dfrac{1}{AH^2}=\dfrac{1}{SA^2}+\dfrac{1}{AO^2}\Rightarrow AH=\dfrac{SA.AO}{\sqrt{SA^2+AO^2}}=\dfrac{a\sqrt{21}}{7}\)
Cho hình chóp S. ABCD có đáy ABCD là hình thoi cạnh a A B C ^ = 60 0 , cạnh bên SA vuông góc với đáy SA = a 3 Tính thể tích của khối chóp S. ABCD
A. a 3 4
B. a 3 3 6
C. a 3 2
D. a 3 3 3
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a; SA=SB=SC=SD=a√2; O là tâm của hình vuông ABCD.
a) C/m (SAC) và (SBD) cùng vuông góc với (ABCD).
b) C/m (SAC) ⊥(SBD)
c) Tính khoảg cách từ S đến (ABCD)
d) Tính góc giữa đường SB và (ABCD).
e) Gọi M là trung điểm của CD, hạ OH⊥SM, chứng minh H là trực tâm tam giác SCD
f) Tính góc giưa hai mặt phẳng (SCD) và (ABCD)
g) Tính khoảng cách giữa SM và BC; SM và AB.
a: SO vuông góc (ABCD)
=>(SAC) vuông góc (ABCD)
SO vuông góc (ABCD)
=>(SBD) vuông góc (ABCD)
b: BD vuông góc AC
BD vuông góc SA
=>BD vuông góc (SAC)
d: (SB;(ABCD))=(BS;BO)=góc SBO
cos SBO=OB/SB=a*căn 2/2/(a*căn 2)=1/2
=>góc SBO=60 độ
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Hình chiếu của S lên mặt phẳng đáy trùng với trọng tâm tam giác ABD. Cạnh bên SD tạo với đáy một góc 60 0
Tính thể tích khối chóp S.ABCD
A. a 3 15 3
B. a 3 15 27
C. a 3 15 9
D. a 3 3
Đáp án C
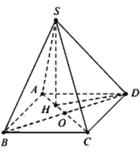
Phương pháp giải:
Xác định hình chiếu của đỉnh, xác định góc để tìm chiều cao và áp dụng công thức thể tích
Lời giải:
Gọi O là tâm hình vuông ABCD , H là trọng tâm tam giác ABD
Ta có ![]()
![]()
ABCD là hình vuông cạnh a nên 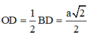
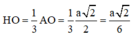
Tam giác HDO vuông tại O, có 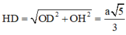
Tam giác SHD vuông tại H, có 
Vậy thể tích cần tính là 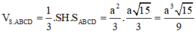
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Hình chiếu của S lên mặt phẳng đáy trùng với trọng tâm tam giác ABD. Cạnh bên SD tạo với đáy một góc 60 0 . Tính thể tích khối chóp S.ABCD
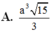
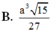

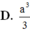
Cho hình chóp S. ABCD có đáy ABCD là hình vuông tâm O cạnh a. SO vuông góc với mặt phẳng (ABCD) và S O = a 2 Tính khoảng cách d giữa SC và AB.
A. d = a 3 5
B. d = a 5 5
C. d = a 2 3
D. d = 2 a 2 3
Cho hình chóp S. ABCD có đáy ABCD là hình vuông tâm O cạnh a. SO vuông góc với mặt phẳng (ABCD) và SO = a 2 Tính khoảng cách d giữa SC và AB.
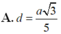
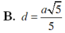
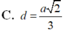
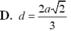
Chọn D
Phương pháp:
Sử dụng lý thuyết d(a,b) = d(a,(P)) = d (M,(P)) với a, b là các đường thẳng chéo nhau, (P) là mặt phẳng chứa chứa b và song song với a, M là một điểm bất kì thuộc a.
Cách giải:
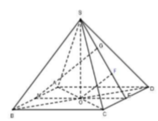
Gọi M, E là trung điểm của AB, CD và F, G là hinh chiếu của O, M lên SE.
Ta thấy:
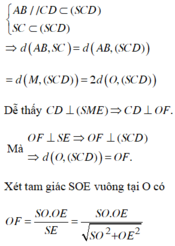
 nhân 2 rồi chọn ngay C là sai.
nhân 2 rồi chọn ngay C là sai.
Cho hình chóp S. ABCD đáy là hình vuông cạnh a, tâm O. Cạnh bên SA=2a và vuông góc với mặt phẳng đáy. Gọi αlà góc tạo bởi đường thẳng SC và mặt phẳng đáy. Mệnh đề nào sau đây đúng?
A. α = 60 ⁰
B. α = 75 ⁰
C. tan α = 1
D. tan α = 2