Cho bất phương trình: 2 x - 13 > 8 9 . Số các nghiệm nguyên của bất phương trình là:
A. 2
B. 3
C. 4
D. 5
Cho bất phương trình x − 1 3 + mx ≤ m − 9 . Tìm x để bất phương trình có nghiệm x = 10 .
Cho tập A = {-10; -9; -8; -7;…..; 8; 9; 10}. Hãy cho biết số nào Cho tập A = {-10; -9; -8; -7;…..; 8; 9; 10}. Hãy cho biết số nào là nghiệm của bất phương trình. |x – 2| ≤ 3
Ta có: |x – 2| ≤ 3
⇔ -3 ≤ x – 2 ≤ 3
⇔ -1 ≤ x ≤ 5
Các số trong tập hợp A là nghiệm của bất phương trình là:
-1; 0; 1; 2; 3; 4; 5
1/ Với giá trị nào của x thì 2 bất phương trình sau đây tương đương: (a-1)x - a+3>0 và ( a+1)x-a+2>0
2/ Bất phương trình: 5x/5 - 13/21 + x/15 < 9/25- 2x/35 có nghiệm là....
3/ Bất phương trình: 5x-1 < 2x/5 + 3 có nghiệm là...
4/ Bất phương trình: (x+4/x^2-9) -(2/x+3) < (4x/3x-x^2) có nghiệm nguyên lớn nhất là...
5/ Các nghiệm tự nhiên bé hơn 4 của bất phương trình (2x/5) -23 < 2x -16
6/ Các nghiệm tự nhiên bé hơn 6 của bất phương trình: 5x - 1/3 > 12 - 2x/3
7/ Bất phương trình: 2(x-1) - x > 3(x-1) - 2x-5 có tập nghiệm là...
8/ Bất phương trình: (3x+5/2) -1< (x+2/3)+x có tập nghiệm là...
9/ Bất phương trình: /x+2/ - /x-1/ < x - 3/2 có tập nghiệm là
10/ Bất phương trình: /x+1/ + /x-4/ > 7 có nghiệm nguyên dương nhỏ nhất là....
hoc gioi the hihiihihihhhihihihihiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiii
,mnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnn
Mình không biết sin lỗi vạn
Cho tập A = {-10; -9; -8; -7;…..; 8; 9; 10}. Hãy cho biết số nào trong A là nghiệm của bất phương trình. |x – 3| > 5
Ta có: |x – 3| > 5
⇒ (x-3 > 5) hoặc (x-3 < -5)
⇔ (x > 8) hoặc (x < -2)
Các số trong tập hợp A là nghiệm của bất phương trình là:
10; 9; -3; -4; -5; -6; -7; -8; -9; -10
Giải các bất phương trình sau và biểu diễn tập nghiệm trên trục số:
a) 2 3 x − 9 > x + 1 3 ; b) 4 x 3 x + 2 − 7 ≤ 3 2 x − 1 2
Giải các bất phương trình: x - 1 4 - 1 > x + 1 3 + 8
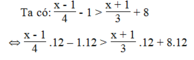
⇔ 3x – 3 – 12 > 4x + 4 + 96
⇔ 3x – 4x > 4 + 96 + 3 + 12
⇔ -x > 115 ⇔ x < -115
Vậy tập nghiệm của bất phương trình là: {x|x < -115}
Bài 1: Cho bất phương trình \(4\sqrt{\left(x+1\right)\left(3-x\right)}\le x^2-2x+m-3\). Xác định m để bất phương trình nghiệm \(\forall x\in[-1;3]\)
Bài 2: Cho bất phương trình \(x^2-6x+\sqrt{-x^2+6x-8}+m-1\ge0\). Xác định m để bất phương trình nghiệm đúng \(\forall x\in[2;4]\)
Câu 1 Mã: 78331
Giải bất phương trình 2x+1x+2≤12x+1x+2≤1
−2≤x≤−1−2≤x≤−1
−2≤x<1−2≤x<1
−2<x≤1−2<x≤1
Vô nghiệm
Câu 2 Mã: 78319
Bất phương trình (3x+1)(6-5x)(3x-7)<0, tập nghiệm của bất phương trình là:
S={x |−13<x<65−13<x<65}
S={x| x>73x>73 }
S={x| −13≤x≤65−13≤x≤65 hoặc x>73x>73 }
S={x| −13<x<65−13<x<65 hoặc x>73x>73 }
Câu 3 Mã: 78314
Tập nghiệm của bất phương trình tích (x+3)(x-7)
S={x\-3 < x hoặc x < 7}
S={x\-3 < x < 7}
S={x\-3 > x > 7}
S={-3;7}
Câu 4 Mã: 78328
Giải bất phương trình: 3xx−3>3x−1x−33xx−3>3x−1x−3
x>−3x>−3
x≥−3x≥−3
x>3x>3
x≥3x≥3
Câu 5 Mã: 78330
Giải bất phương trình: 1x+4≤1x−21x+4≤1x−2
x≥2x≥2
x≤−4x≤−4
x≥2x≥2 hoặc x≤−4x≤−4
x≥2x≥2 vàx≤−4x≤−4
Câu 6 Mã: 78316
Bất phương trình (2x-3)(x22+1)≤0≤0. Tập nghiệm của bất phương trình là:
S={x\x≤32≤32}
S={x\x≥32≥32}
S={x\x<32<32}
Đáp án khác
Câu 7 Mã: 78332
Số nghiệm nguyên thỏa mãn bất phương trình (x+5)(7−2x)>0(x+5)(7−2x)>0
8
7
9
10
Câu 8 Mã: 78321
Tìm x sao cho (x-2)(x-5)>0
x>5 và x<2
x>2
x>5 hoặc x<2
x>5
Câu 9 Mã: 78327
Có bao nhiêu giá trị x nguyên thỏa mãn bất phương trình: x−3x+5+x+5x−3<2x−3x+5+x+5x−3<2
4
5
3
6
Câu 10 Mã: 78315
Cho bất phương trình -2x22+11x-15>0. Giá trị x nguyên thỏa mãn bất phương trình là:
x=3
x=2
x=-2
không có giá trị x nào thỏa mãn
Câu 11 Mã: 78318
Cho bất phương trình: (2x+3)(x+1)(3x+5)≥≥ 0, tập nghiệm của bất phương trình là:
S={x | −53≤x≤−32−53≤x≤−32}
S={x | x≥−1x≥−1}
S={x| −53≤x≤−32−53≤x≤−32 hoặc x≥−1x≥−1}
S={x| −53<x<−32−53<x<−32 hoặc x>−1x>−1}
Câu 12 Mã: 78322
Tìm x sao cho x+2x−5<0x+2x−5<0
−2<x<4−2<x<4
−2<x<5−2<x<5
x<5x<5
x>−2x>−2
Câu 13 Mã: 78326
Giải bất phương trình: 4x+32x+1<24x+32x+1<2
x=−12x=−12
x≠−12x≠−12
x>−12x>−12
x<−12x<−12
Câu 14 Mã: 78313
Tập nghiệm của bất phương trình (x-1)(x+2)>0 là:
S={x/x<1 hoặc x>-2}
S={x/x<-2 hoặc x>1}
S={x/x>1 hoặc x<-2}
S={x/x>-2 hoặc x<1}
Câu 15 Mã: 78320
Bất phương trình (2x+1)(x2−4)>0(2x+1)(x2−4)>0 có tập nghiệm là:
S={x| -2 < x < −12−12 hoặc x>2}
S={x | -2 < x < −12−12 hoặc x≥≥ 2}
S={x | -2≤≤ x < −12−12 hoặc x>2}
S={x | -2 < x < −12−12 hoặc x=2}
Câu 16 Mã: 78329
Giải bất phương trình sau: 3x−4x+2≥03x−4x+2≥0
2<x<122<x<12
−12≤x≤−2−12≤x≤−2
x≤−2x≤−2
2≤x≤122≤x≤12
Câu 17 Mã: 78317
Cho bất phương trình:x2−4x+4≤0x2−4x+4≤0 , tập nghiệm của bất phương trình là:
S={x\x≤≤ 2}
S={2}
S={x\x< 2}
Đáp án khác
Câu 18 Mã: 78325
Tìm nghiệm nguyên dương của bất phương trình:
x2−2x−4(x+1)(x−3)>1x2−2x−4(x+1)(x−3)>1 (1)
x∈{1}x∈{1}
x∈{2}x∈{2}
x∈{1;2}x∈{1;2}
Vô nghiệm
Câu 19 Mã: 78324
Giải bất phương trình: (x−4)(9−x)≥0(x−4)(9−x)≥0
x≥4x≥4
x<9x<9
4≤x≤94≤x≤9
Vô nghiệm
Câu 20 Mã: 78323
Bất phương trình x2−2x+1<9x2−2x+1<9
−2<x<4−2<x<4
−2≤x<4−2≤x<4
−2<x<6−2<x<6
−2<x≤6
Giải bất phương trình: \(\dfrac{8-x}{\sqrt{9-x}}-\dfrac{2-x}{\sqrt{x-1}}\ge3\)
ĐKXĐ: \(1< x< 9\)
Đặt \(\left\{{}\begin{matrix}\sqrt{9-x}=a\\\sqrt{x-1}=b\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a;b>0\\a^2+b^2=8\end{matrix}\right.\) \(\Rightarrow\left(a+b\right)^2\le16\Rightarrow a+b\le4\)
\(BPT\Leftrightarrow\dfrac{a^2-1}{a}+\dfrac{b^2-1}{b}\ge3\) (1)
Đặt \(P=\dfrac{a^2-1}{a}+\dfrac{b^2-1}{b}-3\)
\(P=a+b-\left(\dfrac{1}{a}+\dfrac{1}{b}\right)-3\le a+b-\dfrac{4}{a+b}-3\)
\(P\le\dfrac{\left(a+b\right)^2-3\left(a+b\right)-4}{a+b}=\dfrac{\left(a+b+1\right)\left(a+b-4\right)}{a+b}\le0\)
\(\Rightarrow\dfrac{a^2-1}{a}+\dfrac{b^2-1}{b}\le3\) (2)
(1); (2) \(\Rightarrow\dfrac{a^2-1}{a}+\dfrac{b^2-1}{b}=3\)
Dấu "=" xảy ra khi và chỉ khi: \(a=b=2\Leftrightarrow x=5\)
Vậy BPT đã cho có nghiệm duy nhất \(x=5\)