Cho khối lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác cân tại B. BC = a, A B C ^ = 60 0 , CC' = 4a. Tính thể tích khối A'CC'B'B.
A. a = 2 a 3 3 3
B. a = a 3 3 3
C. a = a 3 3
D. a = 3 a 3
Những câu hỏi liên quan
Cho khối lăng trụ đứng ABC.ABC có đáy ABC là tam giác cân tại B. BC a,
A
B
C
⏜
60
°
, CC 4a. Tính thể tích khối
A
C
C
B
B
. A.
V
2
a
3
3
3
B.
V...
Đọc tiếp
Cho khối lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác cân tại B. BC = a, A B C ⏜ = 60 ° , CC' = 4a. Tính thể tích khối A ' C C ' B ' B .
A. V = 2 a 3 3 3
B. V = a 3 3 3
C. V = a 3 3
D. V = 3 a 3
Đáp án A
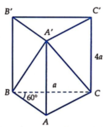
∆ A B C cân có A B C ⏞ = 60 ° ⇒ ∆ A B C đều cạnh a
⇒
V
A
B
C
.
A
'
B
'
C
'
=
S
A
B
C
.
C
C
'
=
1
2
.
a
.
a
.
sin
60
°
.
4
a
=
a
3
3
V
A
'
A
B
C
=
1
3
V
A
B
C
.
A
'
B
'
C
'
=
a
3
3
3
⇒
V
A
'
C
C
'
B
'
B
=
V
A
B
C
.
A
'
B
'
C
'
-
V
A
'
.
A
B
C
=
a
3
3
-
a
3
3
3
=
2
a
3
3
3
Đúng 0
Bình luận (0)
Cho khối lăng trụ đứng ABC.ABC có đáy ABC là tam giác vuông cân tại B với BA BC 2a, đường thẳng AC hợp với đáy một góc
60
°
Tính thể tích khối lăng trụ ABC.ABC là
A
.
V
A
B
C
.
A
B
C
4...
Đọc tiếp
Cho khối lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông cân tại B với BA = BC = 2a, đường thẳng A'C hợp với đáy một góc 60 ° Tính thể tích khối lăng trụ ABC.A'B'C' là
A . V A B C . A ' B ' C ' = 4 a 3 6 3
B . V A B C . A ' B ' C ' = 4 a 3 2 3
C . V A B C . A ' B ' C ' = 4 a 3 2 9
D . V A B C . A ' B ' C ' = 4 a 3 6
![[柠檬]๛Čɦαŋɦ ČŠツ](https://hoc24.vn/images/avt/avt6342624_256by256.jpg)
a) Cho hình lăng trụ đứng ABC.ABC có đáy ABC là tam giác vuông cân tại A, ABa. Biết diện tích tứ giác ABBA bằng 2a^2, thể tích khối lăng trụ ABC.ABC bằng? b) Cho hình lăng trụ đúng ABC.ABC có đáy ABC là tam giác vuông cân tại A, ABa. Biết góc giữa (ABC) và (ABC) bằng 60°, thể tích khối lăng trụ ABC.ABC bằng?
Đọc tiếp
a) Cho hình lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông cân tại A, AB=a. Biết diện tích tứ giác ABB'A' bằng \(2a^2\), thể tích khối lăng trụ ABC.A'B'C' bằng?
b) Cho hình lăng trụ đúng ABC.A'B'C' có đáy ABC là tam giác vuông cân tại A, AB=a. Biết góc giữa (AB'C') và (A'B'C') bằng 60°, thể tích khối lăng trụ ABC.A'B'C' bằng?
a: BB'=2a^2:a=2a
V=BB'*S ABC
=2a*1/2a^2
=a^3
Đúng 0
Bình luận (0)
Cho lăng trụ đứng ABC.ABC có đáy ABC là tam giác vuông cân tại B, BC 2a, AM 3a với M là trung điểm cạnh BC. Thể tích khối lăng trụ ABC.ABC là A.
8
a
3
3
B.
8
a
3
3
C.
16
a
3
3
3...
Đọc tiếp
Cho lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông cân tại B, BC = 2a, A'M = 3a với M là trung điểm cạnh BC. Thể tích khối lăng trụ ABC.A'B'C' là
A. 8 a 3 3
B. 8 a 3 3
C. 16 a 3 3 3
D. 4 a 3
Cho lăng trụ đứng ABC.ABC có đáy ABC là tam giác vuông cân tại B, BC 2a, A’M 3a với M là trung điểm cạnh BC. Thể tích khối lăng trụ ABC.ABC là A.
8
a
3
3
B.
8
a
3
3
C.
16
a
3...
Đọc tiếp
Cho lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông cân tại B, BC = 2a, A’M = 3a với M là trung điểm cạnh BC. Thể tích khối lăng trụ ABC.A'B'C' là
A. 8 a 3 3
B. 8 a 3 3
C. 16 a 3 3 3
D. 4 a 3
Đáp án D
Ta có ABC là tam giác vuông cân tại B
Đúng 0
Bình luận (0)
Cho hình lăng trụ đứng ABC.ABC có đáy ABC là tam giác cân tại A,
B
A
C
^
120
0
,
B
C
A
A
3
a
. Tính thể tích V của khối lăng trụ ABC.ABC. A.
V
9
a
3...
Đọc tiếp
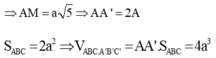
Cho hình lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác cân tại A, B A C ^ = 120 0 , B C = A A ' = 3 a . Tính thể tích V của khối lăng trụ ABC.A'B'C'.
A. V = 9 a 3 4
B. V = 3 3 a 3 2
C. V = 3 3 a 3 6
D. V = 3 a 3 4
Đáp án D
Ta có: B C 2 = A B 2 + A C 2 − 2 A B . A C cos A = 2 A B 2 − 2 A B 2 cos 120 0 = 3 A B 2 ⇒ A B = A C = a
S A B C = 1 2 . a 2 sin 120 0 = 3 a 2 4
. Thể tích lăng trụ là: V = A A ' . S A B C = 3 a . 3 a 2 4 = 3 a 3 4
Đúng 0
Bình luận (0)
Cho hình lăng trụ đứng ABC.ABC có đáy ABC là tam giác cân tại A,
B
A
C
⏜
120
0
, BCAA
3
a
. Tính thể tích V của khối lăng trụ ABC.ABC
Đọc tiếp
Cho hình lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác cân tại A, B A C ⏜ = 120 0 , BC=AA'= 3 a . Tính thể tích V của khối lăng trụ ABC.A'B'C'
Cho hình lăng trụ đứng
A
B
C
.
A
B
C
có đáy ABC là tam giác cân tại A,
B
A
C
^
120
°
,
B
C
A
A
3
a
. Tính theo a thể tích V của khối lăng trụ
A
B
C
.
A
B
C
A. ...
Đọc tiếp
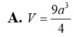
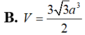
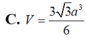
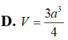
Cho hình lăng trụ đứng A B C . A ' B ' C ' có đáy ABC là tam giác cân tại A, B A C ^ = 120 ° , B C = A A ' = 3 a . Tính theo a thể tích V của khối lăng trụ A B C . A ' B ' C '
A. V = 9 a 3 4
B. V = 3 3 a 3 2
C. V = 3 6 a 3 6
D. V = 3 a 3 4
Đáp án D
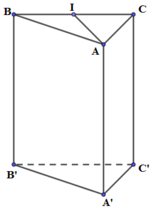
Phương pháp:
Thể tích khối lăng trụ: V = Sh, trong đó: S là diện tích đáy, h là chiều cao.
Cách giải:
Đúng 0
Bình luận (0)
Cho hình lăng trụ đứng ABC.ABC có đáy ABC là tam giác cân tại A, và
BAC
^
120
°
,
BC
AA
3
a
. Tính theo a thể tích V của khối lăng trụ ABC.ABC A.
V
9
a
3
4...
Đọc tiếp
Cho hình lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác cân tại A, và BAC ^ = 120 ° , BC = AA ' = 3 a . Tính theo a thể tích V của khối lăng trụ ABC.A'B'C'
A. V = 9 a 3 4
B. V = 3 3 a 3 6
C. V = 3 3 a 3 2
D. V = 3 a 3 4
