Chọn ngẫu nhiên 3 số tự nhiên từ tập hợp A = 1 , 2 , 3 , . . . , 2019 . Tính xác suất P trong 3 số tự nhiên được chọn không có 2 số tự nhiên liên tiếp.
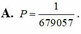
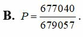
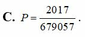
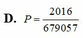
Chọn ngẫu nhiên 3 số tự nhiên từ tập hợp A={1;2;3;…2019}. Tính xác suất P trong 3 số tự nhiên được chọn không có 2 số tự nhiên liên tiếp
A. P = 1 679057
B. P = 677040 679057
C. P = 2017 679057
D. P = 2018 679057
Chọn đáp án B
Phương pháp
+) Tính số phần tử của không gian mẫu.
+) Gọi A là biến cố: “Trong 3 số tự nhiên được chọn không có 2 số tự nhiên liên tiếp”
=> A “Trong 3 số tự nhiên được chọn có 2 số tự nhiên liên tiếp”.
+) Tính số phần tử của biến cố A .
+) Tính xác suất của biến cố A , từ đó tính xác suất biến cố A.
Cách giải
Chọn ngẫu nhiên 3 số tự nhiên ⇒ n Ω = C 2019 3
Gọi A là biến cố: “Trong 3 số tự nhiên được chọn không có 2 số tự nhiên liên tiếp”
=> A : “Trong 3 số tự nhiên được chọn có 2 số tự nhiên liên tiếp”.
Số cách chọn 3 trong 2019 số, trong đó có 2 số tự nhiên liên tiếp, có 2018.2017 cách (có bao gồm các bộ 3 số tự nhiên liên tiếp).
Số cách cả 3 số tự nhiên liên tiếp, có 2017 cách.
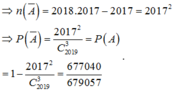
Gọi E là tập hợp các số tự nhiên gồm 3 chữ số phân biệt từ các chữ số 1, 2, 3, 4, 5. Chọn ngẫu nhiên 2 số khác nhau từ tập hợp E. Tính xác suất để 2 số được chọn có đúng 1 số có chữ số 5.
A. 7 22
B. 5 63
C. 144 295
D. 132 271
Gọi E là tập hợp các số tự nhiên gồm 3 chữ số phân biệt từ các chữ số 1, 2, 3, 4, 5. Chọn ngẫu nhiên 2 số khác nhau từ tập hợp E. Tính xác suất để 2 số được chọn có đúng 1 số có chữ số 5
A. 7 22
B. 5 63
C. 144 295
D. 132 271
Gọi A là tập hợp tất cả các số tự nhiên gồm bốn chữ số đôi một khác nhau được chọn từ các chữ số 1; 2; 3; 4; 5; 6. Chọn ngẫu nhiên một số từ tập A. Xác suất để số chọn được là số chia hết cho 5 là
A. 2/3
B. 1/6
C. 1/30
D. 5/6
Gọi A là tập hợp tất cả các số tự nhiên gồm bốn chữ số đôi một khác nhau được chọn từ các chữ số 1 ; 2 ; 3 ; 4 ; 5 ; 6 . Chọn ngẫu nhiên một số từ tập A . Xác suất để số chọn được là số chia hết cho 5 là
A. 2 3 .
B. 1 6 .
C. 1 30 .
D. 5 6 .
Gọi S là tập hợp các số tự nhiên có 6 chữ số được lập từ tập hợp \(A=\left\{0;1;2;3;4;5;6\right\}\). Chọn ngẫu nhiên 1 số từ tập hợp S . Tính xác suất để chọn được số tự nhiên có tích các chữ số bằng 120.
Gọi A là tập hợp các số tự nhiên có 6 chữ số đội một khác nhau được tạo ra từ các chữ số 0, 1, 2, 3, 4, 5. Từ A chọn ngẫu nhiên một số. Tính xác suất để số được chọn có chữ số 3 và 4 đứng cạnh nhau.
A. 4 25
B. 4 15
C. 8 15
D. 2 15
Cho tập hợp A ={1;2;3;4;5}. Gọi B là tập số tự nhiên có 10 chữ số mà các chữ số lấy từ tập hợp A. Chọn ngẫu nhiên một số từ tập hợp B. Tính xác suất để số được chọn có một số lẻ chữ số 1 và một số chẵn chữ số 2.
"Một số lẻ chữ số 1 và 1 số chẵn chữ số 2" nghĩa là sao nhỉ?
Bạn có thể ghi 1 cách chính xác tuyệt đối đề bài không?
Gọi S là tập hợp tất cả các số tự nhiên gồm 3 chữ số phân biệt được chọn từ các chữ số 1, 2, 3, 4, 5, 6, 7. Chọn ngẫu nhiên 1 số từ S, gọi P là xác suất chọn được số chẵn, mệnh đề nào dưới đây đúng?
A. P = 2 7
B. P = 3 5
C. P = 2 5
D. P = 3 7
Đáp án D
Ta thu được số chẵn khi chữ số hàng đơn vị là chắn. Do vai trò của 7 số trong đó có 3 số chẵn là như nhau nên xác suất cần tính bằng 3 7