Trong không gian tọa độ Oxyz, cho ba điểm M ( 1 ; 1 ; 1 ) , N ( 2 ; 3 ; 4 ) , P ( 7 ; 7 ; 5 ) . Để tứ giác MNPQ là hình bình hành thì tọa độ điểm Q là
A. Q(-6;5;2).
B. Q(6;5;2).
C. Q(6;-5;2).
D. Q(-6;-5;-2).
Trong không gian với hệ tọa độ Oxyz, cho 2 điểm A(3;2;-1), B(5;4;3). M là điểm thuộc tia đối của tia BA sao cho A M B M = 2 . Tìm tọa độ của điểm M.
A. (7;6;7)
B. 13 3 ; 10 3 ; 5 3
C. - 5 3 ; - 2 3 ; 11 3
D. (13;11;5)
Đáp án A.
M là điểm thuộc tia đối của tia BA sao cho A M B M = 2 nên B là trung điểm của AM.

Trong không gian với hệ tọa độ Oxyz, cho 2 điểm A(3;2;-1),B(5;4;3). M là điểm thuộc tia đối của tia BA sao cho AM/BM=2. Tìm tọa độ của điểm M
A. (7;6;7)
B. (13/3;10/3;5/3)
C. (-5/3;-2/3;11/3)
D. (13;11;5)
Trong không gian với hệ trục tọa độ Oxyz, cho ba điểm A (3;2;l), B (l;-1;2), C (l;2;-1). Tìm tọa độ điểm M thỏa mãn O M → = 2 A B → - A C →
A. M (-2;6;-4)
B. M (2;-6;4)
C. M (-2;-6;4)
D. M (5;5;0)
Chọn C.
Phương pháp: Hai véc tơ bằng nhau khi và chỉ khi các tọa độ tương ứng bằng nhau.

Trong không gian với hệ trục tọa độ Oxyz, cho ba điểm A (3;2;l), B (l;-1;2), C (l;2;-1). Tìm tọa độ điểm M thỏa mãn O M ⇀ = 2 A B ⇀ - A C ⇀
![]()
![]()
![]()
![]()
Trong không gian tọa độ Oxyz, cho ba điểm M ( 1 ; 1 ; 1 ) , N ( 2 ; 3 ; 4 ) , P ( 7 ; 7 ; 5 ) . Để tứ giác MNPQ là hình bình hành thì tọa độ điểm Q là
A. Q(-6;5;2).
B. Q(6;5;2).
C. Q(6;-5;2).
D. Q(-6;-5;-2).
Trong không gian tọa độ Oxyz cho ba điểm M ( 1 ; 1 ; 1 ) ; N ( 2 ; 3 ; 4 ) ; P ( 7 ; 7 ; 5 ) . Để tứ giác MNPQ là hình bình hành thì tọa độ điểm Q là
A. Q(-6;5;2)
B. Q(6;5;2)
C. Q(6;-5;2)
D. Q(-6;-5;-2)
Chọn B.
Gọi tọa độ điểm Q(x;y;z)
![]()
Vì MNPQ là hình bình hành nên:
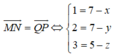
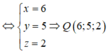
Trong không gian với hệ tọa độ Oxyz , cho ba điểm . Tìm tọa độ điểm D thỏa mãn A D → = 2 A B → + 3 A C →
A. (−10;−17;−7)
B. (10;−17;−7)
C. (10;17;7)
D. (−10;17;−7 )
Trong không gian với hệ tọa độ Oxyz, cho ba điểm A 0 ; 0 ; − 1 , B − 1 ; 1 ; 0 , C 1 ; 0 ; 1 . Tìm điểm M sao cho 3 M A 2 + 2 M B 2 − M C 2 đạt giá trị nhỏ nhất.
A. M 3 4 ; 1 2 ; − 1
B. M − 3 4 ; 1 2 ; 2
C. M − 3 4 ; 3 2 ; − 1
D. M − 3 4 ; 1 2 ; − 1
Đáp án D
Gọi I x I ; y I ; z I thỏa mãn điều kiện 3 I A ¯ + 2 I B ¯ − I C ¯ = 0 ¯ ⇒ I − 3 4 ; 1 2 ; − 1
Ta có P = 3 M A 2 + 2 M B 2 − M C 2 = 3 M I ¯ + I A ¯ 2 + 2 M I → + I B ¯ 2 − M I ¯ + I C ¯ 2
= 4 M I 2 + 2 M I ¯ 3 I A ¯ + 2 I B ¯ − I C ¯ ⏟ 0 + 3 I A 2 + 2 I B 2 − I C 2 = 4 M I 2 + 3 I A 2 + 2 I B 2 − I C 2
Suy ra P min ⇔ M I min ⇒ M trùng với điểm I. Vậy M − 3 4 ; 1 2 ; − 1
Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(1;1;3), B(0;2;1), C(-2;0;-3). Điểm M thuộc Oz sao cho 2 M A → + M B → + M C → nhỏ nhất có tọa độ là:
A. (0;0;2)
B. (0;0;-1)
C. (0;0;1)
D. 0 ; 0 ; 1 2
Đáp án C.
Do M ∈ O z ⇒ M 0 ; 0 ; a ⇒ M A → = 1 ; 1 ; 3 - a , M B → = 0 ; 2 ; 1 - a , M C → = - 2 ; 0 ; - 3 - a
⇒ 2 M A → + M B → + M C → = 0 ; 4 ; - 4 a + 4 ⇒ 2 M A → + M B → + M C → = 4 a - 1 2 + 1 ≥ 4 xảy ra khi a = 1.
Do đó tọa độ điểm M là M(0;0;1).