Chọn hình dưới đây
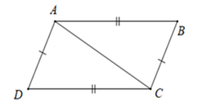
Chọn câu sai
A. AD//BC
B. AB//CD
C. Δ A B C = Δ C D A
D. Δ A B C = Δ A C D
Bài 1: Cho Δ ABC vuông góc tại A có BC = 5cm, AC = 3cm, EF = 3cm, DE = DF = 2,5cm. Chọn phát biểu đúng?
A. Δ ABC ∼ Δ DEF
B. ABCˆ = EFDˆ
C. ACBˆ = ADFˆ
D. ACBˆ = DEFˆ
Bài 2: Cho hai tam giác Δ RSK và Δ PQM có: RS/PQ = RK/PM = SK/QM thì:
A. Δ RSK ∼ Δ PQM
B. Δ RSK ∼ Δ MPQ
C. Δ RSK ∼ Δ QPM
D. Δ RSK ∼ Δ QMP
Bài 3: Nếu Δ RSK ∼ Δ PQM có: RS/PQ = RK/PM = SK/QM thì
A. RSKˆ = PQMˆ
B. RSKˆ = PMQˆ
C. RSKˆ = MPQˆ
D. RSKˆ = QPMˆ
Bài 4: Chọn câu trả lời đúng?
A. Δ ABC, Δ DEF;AB/DE = AC/DF;Bˆ = Eˆ ⇒ Δ ABC ∼ Δ DEF
B. Δ ABC, Δ DEF;AB/DE = AC/DF;Cˆ = Fˆ ⇒ Δ ABC ∼ Δ DEF
C. Δ ABC, Δ DEF;AB/DE = AC/DF;Aˆ = Dˆ ⇒ Δ ABC ∼ Δ DEF
D. Δ ABC, Δ DEF;AB/DE = AC/DF;Aˆ = Eˆ ⇒ Δ ABC ∼ Δ DEF
Bài 5: Cho hình bên, ABCD là hình thang ( AB//CD ) có AB = 12,5cm; CD = 28,5cm; DABˆ = DBCˆ. Tính độ dài đoạn BD gần nhất bằng bao nhiêu?
A. 17,5 B. 18
C. 18,5 D. 19
II. Bài tập tự luận
Bài 1: Tứ giác ABCD có AB = 2cm; BC = 6cm; CD = 8cm; DA = 3cm và BD = 4cm. Chứng minh rằng:
a) Δ BAD ∼ Δ DBC
b) ABCD là hình thang
Trắc nghiệm
Quan sát hình 1 và thực hiện các câu hỏi 11,12,13,14,15
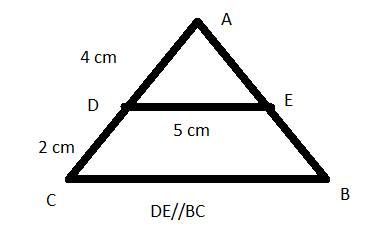
Câu 11:Độ dài cạnh BC là\(\dfrac{AD}{DB}=\dfrac{AD}{AB}\)
A.10 cm B. 5 cm C. 7,5 cm D. 2,5 cm
Câu 12: Tỉ số chu vi của Δ ADE và Δ ABC
A. \(\dfrac{2}{3}\) B. \(\dfrac{3}{2}\) C.\(\dfrac{1}{2}\) D.2
Câu 13 : Tỉ số \(\dfrac{AE}{EC}\) bằng tỉ số nào sau đây:
A. \(\dfrac{3}{2}\) B. \(\dfrac{2}{3}\) C. 2 D.\(\dfrac{1}{2}\)
Câu 14: Khẳng định nào sau đây sai?
A. \(\dfrac{AD}{DB}=\dfrac{AE}{EC}\)\(\) \(\) B. \(\dfrac{AD}{AB}=\dfrac{AE}{AC}\) C. \(\dfrac{BD}{AB}=\dfrac{CE}{AC}\) D.\(\dfrac{BD}{AD}=\dfrac{EC}{AC}\)
Câu 15: Khẳng định nào sau đây đúng?
A.ΔADE∞ΔBAC B.ΔADE∞ΔCAB C.ΔADE∞ΔABC D.ΔADE∞ΔACB
GIÚP MIK VS MIK ĐAG CẦN LỜI GIẢI GẤP![]()
![]() MIK C.ƠN TRC
MIK C.ƠN TRC
Cho tam giác ABC ( AB < AC ) có M là trung điểm của AC. Trên tia đối của tia MB lấy điểm D sao cho MB = MD 1.(MỌI NGƯỜI LÀM GIÚP MÌNH CÂU C,D và VẼ HÌNH NHÉ)
a)Chứng minh Δ A M B = Δ C M D
b) Chứng minh AB = CD và AB || CD .
c)gỌI N là trung điểm của AB.Trên tia đối của tia NC lấy điểm k sao cho NK=NC.Chứng minh DAK thẳng hàng.
d)Vẽ CE vuông gócAD(E thuộc AD)vàÀF vuông gócBC(F thuộcBC).Chứng minh DE=BE
a: Xét ΔAMB và ΔCMD có
MA=MC
góc AMB=góc CMD
MB=MD
Do đó: ΔAMB=ΔCMD
b: ΔAMB=ΔCMD
nên AB=CD và góc MAB=góc MCD
=>AB//CD
c: Xét tứ giác AKBC có
N là trung điểm chung của AB và KC
nên AKBC là hình bình hành
=>AK//BC
Xét tứ giác ABCD có
M là trung điểm chung của AC và BD
nên ABCD là hình bình hành
=>AD//BC
mà AK//BC
nên D,A,K thẳng hàng
1 ) Cho Δ ABC , D là trung điểm của AB . Đường thẳng qua A và song song với BC cắt AC tại E , đường thẳng qua E và song song với AB cắt BC tại F . Chứng mình rằng :
a ) AD = EF
b ) Δ ADE = Δ EFC
c ) AE = EC
2 ) Cho Δ ABC , D là trung điểm của AB , E là trung điểm của AE . Vẽ điểm F sao cho E là trung điểm của DF . Chứng minh rằng :
a ) DB = CF
b ) Δ BDC = Δ FCD
c ) DE // BC và DE = 1/2 BC
Mình sửa lại câu hỏi của mình rồi nha bạn Hải . Bạn làm cả 2 bài giúp mình nhaaaaa
cho Δabc cân tại a có ab=5cm ac=12cm
A.tính bc
B.kéo dài ab lấy d sao cho b là trung điểm ad. nối cd, qua d vẽ đường vuông góc với ad cắt cd tại e. chưng minh Δ dbe=Δ abe và suy ra ade cân
C. kẻ ak vuong góc với bc tại k . qua d kẻ đường thẳng vuông góc với đường thẳng cb tại f . chứng minh b là trung điểm kf
D.chứng minh Δ aec cân và suy ra e là trung điểm của dc
vẽ hình giúp mình với
Cho Δ ABC vuông tại A có góc B=300. Tia phân giác góc C cắt AB tại D. Kẻ DH vuông góc với BC (H ϵ BC).
a) C/m Δ BCD là tam giác cân và Δ ACH là tam giác đều.
b) Khi AB = 5cm. Tính BC, AC
c) Gọi I là giao điểm của HD và AC. C/m Δ IBC là tam giác đều và IC // với AH
Help mik các bạn ơi, please!
cho Δ abc vuông tại A . TIa phân giác góc ABC cắt AC tại D .Vẽ DE vuông góc bc tại E
a, chứng minh Δ adb=Δ edb; ad=de
b,chứng minh AD<BC
c, góc abe cắt bd tại f. chứng minh cf là trung tuyến Δ ace
d, đt vuônggóc bc tại b cắt ca tại m . gọ I là điểm bất kì thuộc ab. trên tia đối be lấy điểm j sao cho AJ=bi, đt vuông gócAB tại I cắt BM tại P . Chứng minh PJ vuông góc JC
Sai đề rùi
Góc ABE ko có cắt BD tại F đc nha!!!
a, xét 2 tam giác vuông ADB và EDB có:
DB cạnh chung
\(\widehat{ABD}\)=\(\widehat{EBD}\)(gt)
=> \(\Delta\)ADB=\(\Delta\)EDB(CH-GN)
=> AD=DE(2 cạnh tương ứng)
b, có sai đề ko vậy, hay là AD<DC
cho góc nhọn xOy. trên tia Ox lấy điểm A và B sao cho OA=OB. Trên tia Oy lấy điểm C và D sao cho OC=OD=OA. Chứng minh rằng
a) Δ OAD = Δ OCB
b) Δ KAB=Δ KCD ( K là giao điểm AD và BC)
c) OK là tia phân giác góc xOy

a) Chứng minh: AD = BC.
Xét ∆OAD và ∆OBC có:
OA = OB (gt);
ˆAODAOD^ chung;
OD = OC (gt)
Do đó ∆OAD = ∆OBC (c.g.c)
Suy ra AD = BC (hai cạnh tương ứng)
b) Chứng minh: ∆EAC = ∆EBD.
Vì ∆OAD = ∆OBC (câu a)
Nên ˆA2=ˆB2A^2=B^2 (hai góc tương ứng)
Mà ˆA1+ˆA2=180oA^1+A^2=180o, ˆB1+ˆB2=180oB^1+B^2=180o (kề bù)
Do đó ˆA1=ˆB1A^1=B^1.
Mặt khác, OA = OB, OC = OD
Suy ra OC – OA = OD – OB
Do đó AC = BD
Xét ∆EAC và ∆EBD có:
ˆA1=ˆB1A^1=B^1 (cmt);
AC = BD (cmt);
ˆOCB=ˆODAOCB^=ODA^ (vì ∆OAD = ∆OBC)
Do đó ∆EAC = ∆EBD (g.c.g).
c) Chứng minh: OE là tia phân giác của góc xOy.
Vì ∆EAC = ∆EBD (câu b)
Nên AE = BE (hai cạnh tương ứng).
Xét ∆OAE và ∆OBE có:
OA = OB (gt);
Cạnh OE chung;
AE = BE (cmt)
Do đó ∆OAE và ∆OBE (c.c.c)
Suy ra ˆAOE=ˆBOEAOE^=BOE^ (hai góc tương ứng)
Hay OE là phân giác của góc xOy.
ai giúp mình đc không ạ ????????????????iu các bạn nhiều lắm các bạn trả lời đúng nha đừng sai đó :D
:))))))))
Bài 1: Cho hình bên, ABCD là hình thang ( AB//CD ) có AB = 12,5cm; CD =
28,5cm; DABˆ = DBCˆ. Tính độ dài đoạn BD gần nhất bằng bao nhiêu?
Bài 2: Tứ giác ABCD có AB = 2cm; BC = 6cm; CD = 8cm; DA = 3cm và BD =
4cm. Chứng minh rằng:
a) Δ BAD ∼ Δ DBC
b) ABCD là hình thang
Bài 3*: Cho hình vẽ như bên, biết EBAˆ = BDCˆ
a) Trong hình vẽ có bao nhiêu tam giác vuông? Kể tên các tam giác vuông đó.
b) Cho AE = 10cm, AB = 15cm, BC = 12cm. Hãy tính độ dài các đoạn thẳng CD,
BE, BD và ED (làm tròn đến chữ số thập phân thứ nhất)
c) So sánh diện tích tam giác BDE với tổng diện tích hai tam giác AEB và BCD
Bài 4: Trên một cạnh của một góc xOy ( Ox ≠ Oy ) đặt các đoạn thẳng OA = 5cm,
OB = 16cm Trên cạnh thứ hai của góc đó đặt các đoạn thẳng OC = 8cm, OD =
10cm.
a) Chứng minh Δ OCB ∼ Δ OAD
b) Gọi I là giao điểm của các cạnh AD và BC. Chứng minh rằng Δ IAB và Δ ICD
có các góc bằng nhau từng đôi một
zồi ôi dài quá
Cho ΔABC cân tại A. Trên AB, AC lấy lần lượt 2 điểm bất kì D, E sao cho AD = AE. Gọi M là trung điểm của BC. Hãy chứng minh:
a) DE // BC
b) ΔMBD = ΔMCE
c) ΔAMD =ΔAME