Cho Δ A B C = Δ D E F . Biết A ^ = 32 0 , F ^ = 78 0 . Tính B ^ ; E ^
A. B ^ = E ^ = 60 0
B. B ^ = 60 0 ; E ^ = 70 0
C. B ^ = E ^ = 78 0
D. B ^ = E ^ = 70 0
Những câu hỏi liên quan
Đồ thị hàm số
y
f
(
x
)
a
x
2
+
b
x
+
c
được cho trong hình 47. Kí hiệu
Δ
b
2
-
4
a
c
là biệt số của f(x). Trong các khẳng định sau, kh...
Đọc tiếp
Đồ thị hàm số y = f ( x ) = a x 2 + b x + c được cho trong hình 47. Kí hiệu Δ = b 2 - 4 a c là biệt số của f(x). Trong các khẳng định sau, khẳng định nào sai?
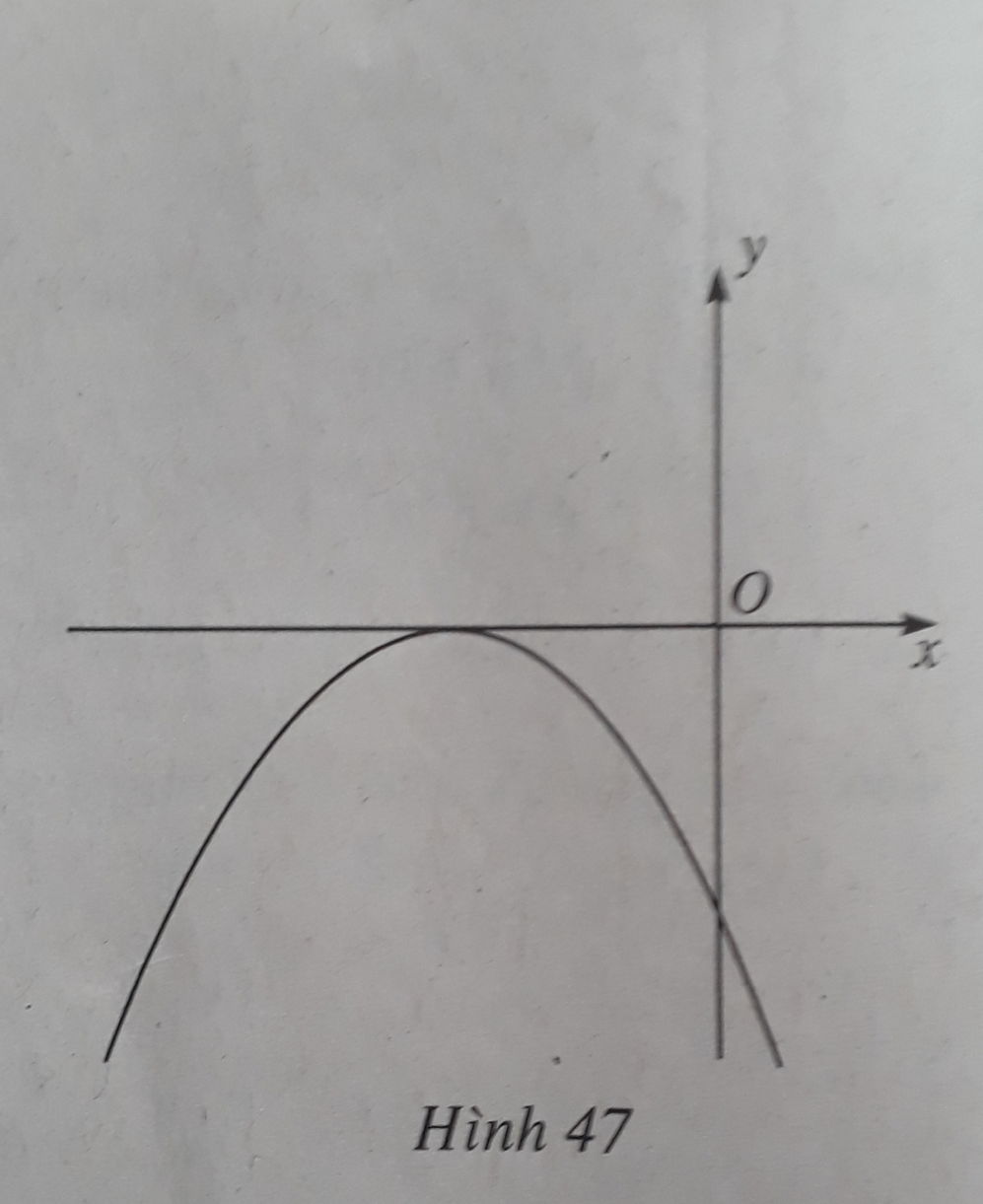
A. a, b trái dấu
B. f(x) ≤ 0, ∀x
C. a < 0, c < 0
D. Δ = 0, a < 0
1 ) Cho Δ ABC , D là trung điểm của AB . Đường thẳng qua A và song song với BC cắt AC tại E , đường thẳng qua E và song song với AB cắt BC tại F . Chứng mình rằng : a ) AD EFb ) Δ ADE Δ EFCc ) AE EC2 ) Cho Δ ABC , D là trung điểm của AB , E là trung điểm của AE . Vẽ điểm F sao cho E là trung điểm của DF . Chứng minh rằng :a ) DB CFb ) Δ BDC Δ FCDc ) DE // BC và DE 1/2 BC
Đọc tiếp
1 ) Cho Δ ABC , D là trung điểm của AB . Đường thẳng qua A và song song với BC cắt AC tại E , đường thẳng qua E và song song với AB cắt BC tại F . Chứng mình rằng :
a ) AD = EF
b ) Δ ADE = Δ EFC
c ) AE = EC
2 ) Cho Δ ABC , D là trung điểm của AB , E là trung điểm của AE . Vẽ điểm F sao cho E là trung điểm của DF . Chứng minh rằng :
a ) DB = CF
b ) Δ BDC = Δ FCD
c ) DE // BC và DE = 1/2 BC
Mình sửa lại câu hỏi của mình rồi nha bạn Hải . Bạn làm cả 2 bài giúp mình nhaaaaa
Đúng 0
Bình luận (0)
Cho Δ ABC vuông tại B. Tia phân giác của góc A cắt BC tại D ( D thuộc BC). Trên cạnh AC lấy điểm E sao cho AE=AB.
a. Chứng minh: Δ ADB = Δ ADE
B. Chứng minh: DB=DE và DE vuông góc AC
c. Trên tia AB lấy điểm F sao cho AF=AC.
Chứng minh : Ba điểm E,D,F thẳng hàng
giải thích dùm mình câu c. lun nha . cảm ơn nhiều
a: Xét ΔABD và ΔAED có
AB=AE
\(\widehat{BAD}=\widehat{EAD}\)
AD chung
Do đó: ΔABD=ΔAED
b: Ta có: ΔABD=ΔAED
nên DB=DE và \(\widehat{ABD}=\widehat{AED}=90^0\)
hay DE\(\perp\)AC
c: Xét ΔDBF vuông tại B và ΔDEC vuông tại E có
DB=DE
BF=EC
Do đó: ΔDBF=ΔDEC
Suy ra: \(\widehat{BDF}=\widehat{EDC}\)
=>\(\widehat{BDF}+\widehat{BDE}=180^0\)
hay F,D,E thẳng hàng
Đúng 0
Bình luận (0)
Cho Δ ABC vuông tại B. Tia phân giác của góc A cắt BC tại D ( D thuộc BC). Trên cạnh AC lấy điểm E sao cho AE=AB.
a. Chứng minh: Δ ADB = Δ ADE
B. Chứng minh: DB=DE và DE vuông góc AC
c. Trên tia AB lấy điểm F sao cho AF=AC.
Chứng minh : Ba điểm E,D,F thẳng hàng
giải thích dùm mình câu c. lun nha . cảm ơn nhiều
a: Xét ΔADB và ΔADE có
AB=AE
\(\widehat{BAD}=\widehat{EAD}\)
AD chung
Do đó: ΔABD=ΔAED
b: Ta có: ΔABD=ΔAED
nên DB=DE và \(\widehat{ABD}=\widehat{AED}=90^0\)
hay DE\(\perp\)AC
c: Xét ΔBDF vuông tại B và ΔEDC vuông tại E có
DB=DE
BF=EC
Do đó: ΔBDF=ΔEDC
Suy ra: \(\widehat{BDF}=\widehat{EDC}\)
=>\(\widehat{BDF}+\widehat{BDE}=180^0\)
hay F,D,E thẳng hàng
Đúng 0
Bình luận (0)
Cho Δ ABC vuông tại B. Tia phân giác của góc A cắt BC tại D ( D thuộc BC). Trên cạnh AC lấy điểm E sao cho AE=AB.
a. Chứng minh: Δ ADB = Δ ADE
B. Chứng minh: DB=DE và DE vuông góc AC
c. Trên tia AB lấy điểm F sao cho AF=AC.
Chứng minh : Ba điểm E,D,F thẳng hàng
giải thích dùm mình câu c. lun nha . cảm ơn nhiều
tam giác abc vuông tại a, phân giác góc b cắt ac tại d, trên cạnh bc lấy e sao cho be=ba. Chứng minh :
a, Δ ABD= Δ EBD
b, DE vuông góc với BC
c, gọi F là giao điểm của ED và AB
Chứng minh ΔABC=Δ EBD
d, CM Δ ADF=Δ EDC
e, CM FC song song với AE
giúp mk với !!!!
Xét ΔABD và ΔEBD, ta có:
AB=BE ( gt)
Góc ABD= góc EBD ( Vì BD là tia phân giác của góc B)
BD chung
⇒ΔABD=ΔEBD(c-g-c)
b)Vì ΔABD=ΔEBD nên góc BAD= góc BED=90 độ( 2 cạnh tương ứng)
hay DE vuông góc với BC
c) Vì ΔABD=ΔEBD nên DA=DE ( 2 cạnh tương ứng)
Xét ΔADF và ΔEDC ta có:
góc FAD=góc CED(câu b)
AD=ED (cmt)
góc ADF=gócEDC( đối đỉnh)
⇒ΔADF=ΔEDC (g-c-g)
d,Xét ΔDAE và ΔDCF có:
DA=DC
Góc ADE=góc CDF (đối đỉnh)
DE=DF
⇒ΔDAE = ΔDCF (c-g-c)
⇒góc DAE=góc DCF (2 góc tương ứng)
MÀ 2 góc này ở vị trí SLT
⇒AE//CF
Đúg thì k
Mè sai cx k hộ nhen
Cho Δ ABC, lấy điểm D thuộc cạnh BC ( D không trùng với B,C). Gọi M là trung điểm của AD. Trên tia đối của tia MB lấy điểm E sao cho ME= MB, trên tia đối của tia MC lấy điểm F sao cho MF= MC. Chứng minh rằng:
a) Δ AME = Δ DMB; AE // BC
b) Ba điểm E, A, F thẳng hàng
c) BF // CE
Bài 5. Cho Δ ABC có AB >AC, đường cao AH, D, E, F thứ tự là trung điểm của AB, BC, AC.
a)Tứ giác DECF là hình gì? Vì sao? b) Δ ABC cần điều kiện gì để DECF là hình chữ nhật c) Cho DE = 13cm, AH = 10cm. Tính diện tích Δ ABCHộ ak
a: Xét ΔABC có
D,F lần lượt là trung điểm của AB,AC
nên DF là đường trug bình
=>DF//BC và FD=1/2BC
=>DF//EC và FD=EC
=>DFCE là hình bình hành
b: Để DFCE là hình chữ nhật thì góc C=90 độ
Đúng 2
Bình luận (0)
Cho tam giác ABC vuông tại A (AB AC). Kẻ AH vuông góc vói BC tại H. Gọi E và F lần lượt là hình chiếu của H trên AB và AC.a) Chứng minh AH2 - AE.AB.b) Chứng minh Δ A F E ~ Δ A B C ;c) Lấy M đối xứng với A qua E, tia MH cắt cạnh AC tại N. Chứng minh A B H ^ A N H ^ và EF//HN.d) Gọi O là trung điểm của BC; AO giao với HN tại K. Cho biết A C B ^ 30 ° , hãy tính tỉ số A K A N S H C A
Đọc tiếp
Cho tam giác ABC vuông tại A (AB < AC). Kẻ AH vuông góc vói BC tại H. Gọi E và F lần lượt là hình chiếu của H trên AB và AC.
a) Chứng minh AH2 - AE.AB.
b) Chứng minh Δ A F E ~ Δ A B C ;
c) Lấy M đối xứng với A qua E, tia MH cắt cạnh AC tại N. Chứng minh A B H ^ = A N H ^ và EF//HN.
d) Gọi O là trung điểm của BC; AO giao với HN tại K. Cho biết A C B ^ = 30 ° , hãy tính tỉ số A K A N S H C A
a: ΔAHB vuông tại H có HE là đường cao
nên AH^2=AE*AB
b: ΔAHC vuông tại H có HF là đường cao
nên AH^2=AF*AC
=>AE*AB=AF*AC
=>AE/AC=AF/AB
Xét ΔAEF vuông tại A và ΔACB vuông tại A có
AE/AC=AF/AB
=>ΔAEF đồng dạng với ΔACB
Đúng 0
Bình luận (0)
Cho Δ ABC vuông tại A , đường cao AH ( H thuộc BC )
a) Tính BH , AH biết AB =20cm ,BC=25cm
b) Từ B kẻ đường thẳng vuông góc với đường trung tuyến AD của tam giác ABC tại E cắt AC tại F . Chứng Minh Δ BHF đồng dạng với Δ BEC
giải chi tiết giúp mk vớiiiiii ạ