Dùng định nghĩa hai phân thức bằng nhau chứng tỏ rằng:
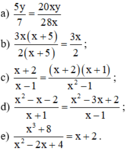
Dùng định nghĩa hai phân thức bằng nhau chứng tỏ rằng:
-
Dùng định nghĩa hai phân thức bằng nhau chứng tỏ rằng:
- Chứng Tỏ Rằng J Hả Bạn ??????
\(a.\frac{5y}{7}=\frac{20xy}{28x}\)
\(b.\frac{3x\left(x+5\right)}{2\left(x+5\right)}=\frac{3x}{2}\)
Dùng định nghĩa hai phân thức bằng nhau chứng minh các đẳng thức sau:
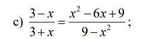
\(\dfrac{3-x}{3+x}=\dfrac{\left(3-x\right)^2}{\left(3-x\right)\left(3+x\right)}=\dfrac{x^2-6x+9}{9-x^2}\)
Dùng định nghĩa 2 phân thức bằng nhau chứng tỏ rằng: 1)1-x/2-y=x-1/y-2 2)2a/-5b=-2a/5b 3)x-2 /-x=2^3-x^3/x (x^2+2x+4)
Dùng định nghĩa hai phân thức bằng nhau chứng minh các đẳng thức sau:
x 2 y 3 5 = 7 x 3 y 4 35 x y
Ta có:
x 2 y 5 . 35 x y = 35 x 3 y 4 5 . 7 x 3 y 4 = 35 x 3 y 4 S u y r a : x 2 y 3 . 35 x y = 5 . 7 x 3 y 4
Vậy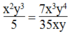
Dùng định nghĩa hai phân thức bằng nhau chứng minh các đẳng thức sau:
x 3 - 4 x 10 - 5 x = - x 2 - 2 x 5
Ta có: x 3 - 4 x . 5 = 5 x 3 - 20 x
10 - 5 x - x 2 - 2 x = - 10 x 2 - 20 x + 5 x 3 + 10 x 2 = 5 x 3 - 20 x
Suy ra: x 3 - 4 x . 5 = 10 - 5 x - x 2 - 2 x
Vậy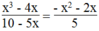
Dùng định nghĩa hai phân thức bằng nhau chứng minh các đẳng thức sau:
x 2 x + 2 x x + 2 2 = x x + 2
Ta có:
x 2 x + 2 x + 2 = x 2 x + 2 2 x x + 2 2 . x = x 2 x + 2 2 S u y r a : x 2 x + 2 x + 2 = x 2 x + 2 2
vậy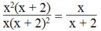
Dùng định nghĩa hai phân thức bằng nhau chứng minh các đẳng thức sau:
3 - x 3 + x = x 2 - 6 x + 9 9 - x 2
Ta có:
3 - x . 9 - x 2 = 3 - x 3 - x 3 + x = 3 - x 2 1)
Và 3 + x x 2 - 6 x + 9 = 3 + x . x - 3 2 = 3 + x . 3 - x 2 (2)
( vì ( x- 3) = - (3- x) nên x - 3 2 = - 3 - x 2 = 3 - x 2 )
Từ (1) và (2) suy ra: x - 3 . 9 - x 2 = 3 + x x 2 - 6 x + 9
Do đó: 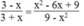
Dùng định nghĩa chứng minh hai phân thức bằng nhau chứng tỏ rằng:
\(\dfrac{x^3+8}{x^2-2x+4}\)= x+2
Ta có: \(\dfrac{x^3+8}{x^2-2x+4}=x+2\)
\(\Rightarrow\left(x^3+8\right)=\left(x^2-2.x+2^2\right)\left(x+2\right)\)
\(\Rightarrow x^3+8=x^3+8\)
\(\rightarrowđpcm.\)
Ta có : \(\dfrac{x^3+2^3}{x^2-2x+4}=\dfrac{\left(x+2\right)\left(x^2-2x+4\right)}{x^2-2x+4}=x+2\left(đpcm\right)\)
\(\dfrac{x^3+8}{x^2-2x+4}=x+2\)
\(\rightarrow\left(x^2-2x+4\right)\left(x+2\right)=x^3+8\)
\(\rightarrow x^3+8=x^3+8\left(đpcm\right)\)
Dùng tính chất cơ bản của phân thức chứng tỏ rằng các cặp phân thức sau bằng nhau: x 2 + 3 x + 2 3 x + 6 v à 2 x 2 + x - 1 6 x - 3