Cho hình lăng trụ đứng ABCD.A'B'C'D' có đáy ABCD là hình thang vuông A ^ = D ^ = 90 0 . Có bao nhiêu cạnh song song với mặt phẳng ( BCC'B' )
A. 3
B. 4
C. 5
D. 6
Những câu hỏi liên quan
Cho hình lăng trụ đứng ABCD.A'B'C'D' có đáy ABCD là hình thang vuông A ^ = D ^ = 90 0 . Có bao nhiêu cạnh vuông góc với mặt phẳng ( BCC'B' ) ?
A. 2
B. 3
C. 4
D. 5
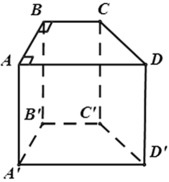
Vì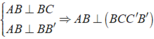
Tương tự: A'B' ⊥ ( BCC'B' ) ⇒ AB,A'B' ⊥ ( BCC'B' )
Chọn đáp án A.
Đúng 0
Bình luận (0)
SGK Chân trời sáng tạo
20 tháng 8 2023 lúc 21:10
Cho hình lăng trụ đứng \(ABCD.A'B'C'D'\) có đáy \(ABCD\) là hình thang vuông tại \(A\) và \(B\), \(AA' = 2a,AD = 2a,AB = BC = a\).
a) Tính độ dài đoạn thẳng \(AC'\).
b) Tính tổng diện tích các mặt của hình lăng trụ.
a) \(\Delta ABC\) vuông cân tại \(B \Rightarrow AC = \sqrt {A{B^2} + B{C^2}} = a\sqrt 2 \)
\(CC' = AA' = 2a\)
\(CC' \bot \left( {ABCD} \right) \Rightarrow CC' \bot AC\)
\( \Rightarrow \Delta ACC'\) vuông tại \(C \Rightarrow AC' = \sqrt {A{C^2} + CC{'^2}} = a\sqrt 6 \)
b) \({S_{ABC{\rm{D}}}} = {S_{A'B'C'C'}} = \frac{1}{2}\left( {A{\rm{D}} + BC} \right).AB = \frac{{3{a^2}}}{2}\)
Gọi \(M\) là trung điểm của \(AD\)
\( \Rightarrow ABCM\) là hình vuông\( \Rightarrow MC = M{\rm{D}} = MA = \frac{1}{2}A{\rm{D}} = a\)
\(\Delta MC{\rm{D}}\) vuông cân tại \(M \Rightarrow C{\rm{D}} = \sqrt {C{M^2} + D{M^2}} = a\sqrt 2 \)
\(\begin{array}{l}{S_{ABB'A'}} = AB.AA' = 2{a^2}\\{S_{ADD'A'}} = AD.AA' = 4{a^2}\\{S_{BCC'B'}} = BC.CC' = 2{a^2}\\{S_{C{\rm{DD}}'{\rm{C}}'}} = C{\rm{D}}.CC' = 2{a^2}\sqrt 2 \end{array}\)
Tổng diện tích các mặt của hình lăng trụ là:
\(\begin{array}{l}S = {S_{ABC{\rm{D}}}} + {S_{A'B'C'C'}} + {S_{ABB'A'}} + {S_{ADD'A'}} + {S_{BCC'B'}} + {S_{C{\rm{DD}}'{\rm{C}}'}}\\ & = \frac{{3{a^2}}}{2} + \frac{{3{a^2}}}{2} + 2{a^2} + 4{a^2} + 2{a^2} + 2{a^2}\sqrt 2 = \left( {11 + 2\sqrt 2 } \right){a^2}\end{array}\)
Đúng 0
Bình luận (0)
Cho lăng trụ đứng ABCD.ABCD có đáy ABCD là hình vuông cạnh a. Mặt phẳng (CBD) hợp với đáy góc
45
∘
. Tính thể tích lăng trụ
Đọc tiếp
Cho lăng trụ đứng ABCD.A'B'C'D' có đáy ABCD là hình vuông cạnh a. Mặt phẳng (C'BD) hợp với đáy góc 45 ∘ . Tính thể tích lăng trụ
Cho lăng trụ đứng ABCD.ABCD có đáy ABCD là hình vuông cạnh a. Mặt phẳng
C
B
D
hợp với đáy góc
45
o
. Tính thể tích lăng trụ A.
V
a
3
B.
V
a
3
2
C.
V
a...
Đọc tiếp
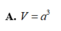
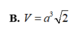
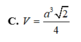
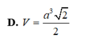
Cho lăng trụ đứng ABCD.A'B'C'D' có đáy ABCD là hình vuông cạnh a. Mặt phẳng C ' B D hợp với đáy góc 45 o . Tính thể tích lăng trụ
A. V = a 3
B. V = a 3 2
C. V = a 3 2 4
D. V = a 3 2 2
Ta có
C ' C ⊥ A B C D , B D ⊥ O C ⇒ B D ⊥ O C ' ⇒ C O C ' ^ = 45 o
∆ O C C ' vuông cân tại C ⇒ C C ' = O C = a 2 2
Vậy V = a 2 . a 2 2 = a 3 2 2
Đáp án D
Đúng 0
Bình luận (0)
Lăng trụ đứng ABCD.ABCD có đáy ABCD là hình vuông cạnh a và đường chéo BD của lăng trụ hợp với đáy ABCD một góc 30º. Thể tích của lăng trụ là: A.
a
3
6
3
B.
a
3
6
8
C. ...
Đọc tiếp
Lăng trụ đứng ABCD.A'B'C'D' có đáy ABCD là hình vuông cạnh a và đường chéo BD' của lăng trụ hợp với đáy ABCD một góc 30º. Thể tích của lăng trụ là:
A. a 3 6 3
B. a 3 6 8
C. a 3 3
D. 3 a 3 6
Lăng trụ đứng ABCD.ABCD có đáy ABCD là hình vuông cạnh a và đường chéo BD của lăng trụ hợp với đáy ABCD một góc 30º. Thể tích của lăng trụ là: A
.
a
3
6
3
B
.
a
3
6
8
C
.
a...
Đọc tiếp
Lăng trụ đứng ABCD.A'B'C'D' có đáy ABCD là hình vuông cạnh a và đường chéo BD' của lăng trụ hợp với đáy ABCD một góc 30º. Thể tích của lăng trụ là:
A . a 3 6 3
B . a 3 6 8
C . a 3 3
D . 3 a 3 6
Cho lăng trụ đứng ABCD.ABCD có đáy ABCD là hình thang, AB AD a, CD 2a. Đường thẳng A’C tạo với mặt phẳng (ABCD) một góc bằng 60o. Biết hình lăng trụ nội tiếp một hình trụ. Tính thể tích khối trụ ngoại tiếp lăng trụ theo a ta được: A.
3
πa
3
B.
πa
3
C.
4
πa
3...
Đọc tiếp
Cho lăng trụ đứng ABCD.A'B'C'D có đáy ABCD là hình thang, AB = AD = a, CD = 2a. Đường thẳng A’C tạo với mặt phẳng (ABCD) một góc bằng 60o. Biết hình lăng trụ nội tiếp một hình trụ. Tính thể tích khối trụ ngoại tiếp lăng trụ theo a ta được:
A. 3 πa 3
B. πa 3
C. 4 πa 3 3
D. πa 3 3
Đáp án A
Từ giả thiết ta có hình thang ABCD là hình thang nội tiếp được đường tròn nên nó là hình thang cân AB = AD = BC = a
Khi đó tâm đường tròn ngoại tiếp hình thang ABCD là trung điểm I của CD và bán kính là r = a.
Ta có:
=> A'A = a 3 . 3 = 3a => V = 3π a 3
Đúng 0
Bình luận (0)
Cho lăng trụ đứng ABCD.ABCD (như hình 1) có đáy ABCD là hình thang vuông tại A và B. Biết BC 10 cm, AB AD 5 cm, AA 8 cm.a) Tính diện tích toàn phần lăng trụ (làm tròn đến chữ sô hàng phần trăm).b) Người ta ghép thêm một hình lăng trụ đứng tam giác MNP.MNP vào hình lăng trụ 1 để được một lăng trụ đứng tam giác (như ở hình 2). Tính thể tích hình lăng trụ đứng sau khi ghép biết tam giác MNP vuông tại N và MN 5 cm, MP 5
2
c
m
, MM 8 cm.
Đọc tiếp
Cho lăng trụ đứng ABCD.A'B'C'D' (như hình 1) có đáy ABCD là hình thang vuông tại A và B. Biết BC = 10 cm, AB = AD = 5 cm, AA' = 8 cm.
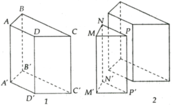
a) Tính diện tích toàn phần lăng trụ (làm tròn đến chữ sô' hàng phần trăm).
b) Người ta ghép thêm một hình lăng trụ đứng tam giác MNP.M'N'P' vào hình lăng trụ 1 để được một lăng trụ đứng tam giác (như ở hình 2). Tính thể tích hình lăng trụ đứng sau khi ghép biết tam giác MNP vuông tại N và MN = 5 cm, MP = 5 2 c m , MM' = 8 cm.
Cho hình lăng trụ đứng ABCD.ABCD có hai đáy là các hình vuông tâm O và tâm O, AB 5 cm và AC ’ 15 cm.a) Hình lăng trụ đứng đã cho có phải hình lập phương không? Vì sao?b) Chứng minh đường thẳng OO vuông góc vói mặt phẳng (ABCD).c) Tìm giao tuyến của hai mặt phẳng (ACCA) và (BDDB’).d) Tính chiều cao của hình lăng trụ đứng
Đọc tiếp
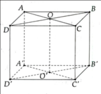
Cho hình lăng trụ đứng ABCD.A'B'C'D' có hai đáy là các hình vuông tâm O và tâm O', AB = 5 cm và AC ’ = 15 cm.
a) Hình lăng trụ đứng đã cho có phải hình lập phương không? Vì sao?
b) Chứng minh đường thẳng OO' vuông góc vói mặt phẳng (ABCD).
c) Tìm giao tuyến của hai mặt phẳng (ACC'A') và (BDD'B’).
d) Tính chiều cao của hình lăng trụ đứng
a) Không vì AA' ≠ AB.
b) HS tự chứng minh.
c) Giao tuyến là OO'.
d) Chiều cao là 5 7 c m
Đúng 0
Bình luận (0)