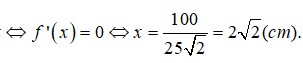Cắt từ tấm bìa cứng thành các hình như ở hình 118 rồi gấp lại để có những hình chóp đều.

Những câu hỏi liên quan
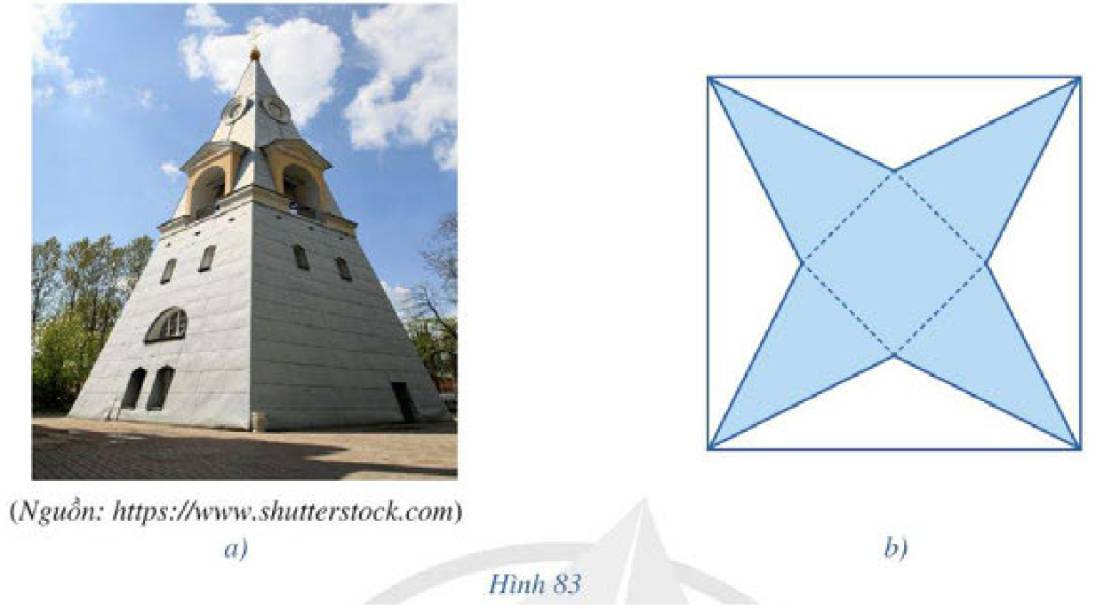
Để tạo mô hình một tháp chuông ở Hình 83a từ một tấm bìa hình vuông, bạn Dũng cắt bỏ phần màu trắng gồm bốn tam giác cân bằng nhau có đáy là các cạnh của tấm bìa (Hình 83b) rồi gấp lại phần màu xanh để tạo thành một hình chóp tứ giác. Quan sát Hình 83a, 83b và cho biết:a) Đáy của hình chóp mà bạn Dũng tạo ra là tứ giác có tính chất gì;b) Các cạnh bên của hình chóp đó có bằng nhau hay không.
Đọc tiếp
Để tạo mô hình một tháp chuông ở Hình 83a từ một tấm bìa hình vuông, bạn Dũng cắt bỏ phần màu trắng gồm bốn tam giác cân bằng nhau có đáy là các cạnh của tấm bìa (Hình 83b) rồi gấp lại phần màu xanh để tạo thành một hình chóp tứ giác. Quan sát Hình 83a, 83b và cho biết:
a) Đáy của hình chóp mà bạn Dũng tạo ra là tứ giác có tính chất gì;
b) Các cạnh bên của hình chóp đó có bằng nhau hay không.
a: Tứ giác đó là hình vuông
b: Các cạnh bên của hình chóp đó bằng nhau
Đúng 0
Bình luận (0)
Trong các tấm bìa ở hình 121, em gấp lại tấm bìa nào thì có được một hình chóp đều?
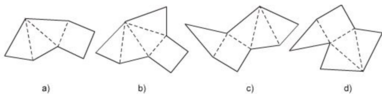
Hình a khi gấp lại thì không được một hình chóp đều vì đáy là tứ giác đều nhưng chỉ có ba mặt bên thay vì phải có 4 mặt bên.
Hình b, c khi gấp lại thì được một hình chóp tứ giác đều.
Hình d khi gấp lại thì không được một hình chóp tứ giác đều vì ở trên cùng một cạnh đáy có đến 2 mặt bên còn trên một cạnh đáy thì không có mặt bên nào.
Đúng 0
Bình luận (0)
Tạo lập hình chóp tam giác đều có độ dài cạnh đáy 3cm và cạnh bên 4cm theo hướng dẫn sau:- Trên một tấm bìa, vẽ một hình tam giác đều và ba hình tam giác cân với kích thước như Hình 7a.- Cắt tấm bìa như hình vẽ, rồi gấp theo các đường màu đỏ ta được hình chóp tam giác đều như Hình 7b.
Đọc tiếp
Tạo lập hình chóp tam giác đều có độ dài cạnh đáy 3cm và cạnh bên 4cm theo hướng dẫn sau:
- Trên một tấm bìa, vẽ một hình tam giác đều và ba hình tam giác cân với kích thước như Hình 7a.
- Cắt tấm bìa như hình vẽ, rồi gấp theo các đường màu đỏ ta được hình chóp tam giác đều như Hình 7b.
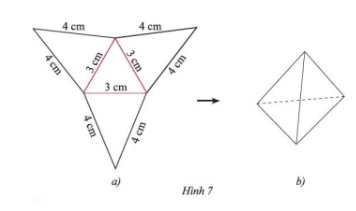
Sau khi thực hiện theo hướng dẫn, ta được sản phẩm như hình 7b.
Đúng 0
Bình luận (0)
Trong các tấm bìa ở hình 56, em gấp lại tấm bìa nào thì có được một hình chóp đều ?
Hình a, khi gấp lại thì không được một hình chóp đều vì đáy là tứ giác đều nhưng chỉ có ba mặt bên thay vì phải có 4 mặt bên.
Hình b, c khi gấp lại thì được một hình chóp tứ giác đều.
Hình d, khi gấp lại thì không được một hình chóp tứ giác đều vì ở trên cùng một cạnh đáy có đến 2 mặt bên còn trên một cạnh đáy thì không có mặt bên nào.
Đúng 0
Bình luận (0)
Tạo lập hình chóp tứ giác đều có độ dài cạnh đáy 4cm và cạnh bên 5cm theo hướng dẫn sau:- Trên một tấm bìa, vẽ một hình vuông và bốn hình tam giác cân với kích thước như Hình 9a.- Cắt tấm bìa như hình vẽ, rồi gấp theo các đường màu đỏ ta được hình chóp tứ giác đều như Hình 9b.
Đọc tiếp
Tạo lập hình chóp tứ giác đều có độ dài cạnh đáy 4cm và cạnh bên 5cm theo hướng dẫn sau:
- Trên một tấm bìa, vẽ một hình vuông và bốn hình tam giác cân với kích thước như Hình 9a.
- Cắt tấm bìa như hình vẽ, rồi gấp theo các đường màu đỏ ta được hình chóp tứ giác đều như Hình 9b.
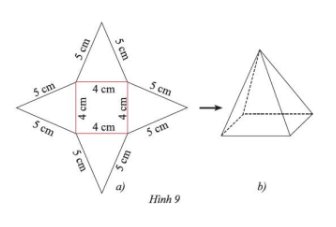
Sau khi thực hiện theo hướng dẫn, ta được sản phẩm như Hình 9b.
Đúng 0
Bình luận (0)
Trong các tấm bìa ở Hình 1, tấm bìa nào gấp được hình chóp tam giác đều, tấm bìa nào gấp được hình chóp tứ giác đều?
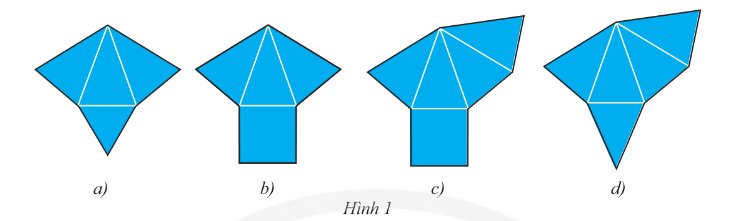
1a gấp được thành hình chóp tam giác đều
1c gấp được thành hình chóp tứ giác đều
Đúng 1
Bình luận (0)
Hình `a,c` có thể gấp được tứ giác đều.
Đúng 0
Bình luận (0)
Từ một tấm bìa hình vuông ABCD có cạnh bằng 5dm, người ta cắt bỏ bốn tam giác bằng nhau là
A
M
B
,
B
N
C
,
C
P
D
và DQA. Với phần còn lại, người ta gấp lên và ghép lại để thành hình chóp tứ giác đều. Hỏi cạnh đáy của khối chóp bằng bao nhiêu để thể tích của nó là lớn nhất? A.
3
2
2
d...
Đọc tiếp
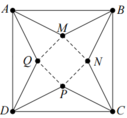
Từ một tấm bìa hình vuông ABCD có cạnh bằng 5dm, người ta cắt bỏ bốn tam giác bằng nhau là A M B , B N C , C P D và DQA. Với phần còn lại, người ta gấp lên và ghép lại để thành hình chóp tứ giác đều. Hỏi cạnh đáy của khối chóp bằng bao nhiêu để thể tích của nó là lớn nhất?
A. 3 2 2 d m
B. 5 2 d m
C. 2 2 d m
D. 5 2 2 d m
Đáp án C
Giả sử M N = x ⇒ d A ; M Q = 5 2 − x 2 0 < x < 5 2
Chiều cao hình chóp là h = 5 2 − x 2 2 − x 2 2 = 50 − 10 x 2 4
Ta có V = 1 3 M N 2 . h = 1 3 x 2 50 − 10 x 2 4 = 1 6 50 x 4 − 10 x 5 2
Đặt
f x = 50 x 4 − 10 x 5 2 ⇒ f ' x = 2 − − x 3 − 50 x 3 2 = 0 ⇒ x = 2 2 d m
Lập bảng BTT suy ra V m a x = 2 2 d m
Đúng 0
Bình luận (0)
Từ một tấm bìa hình vuông ABCD có cạnh bằng 5 dm, người ta cắt bỏ bốn tam giác bằng nhau là AMB, BNC, CPD, DQA. Với phần còn lại, người ta gấp lên và ghép lại để thành hình chóp tứ giác đều. Hỏi cạnh đáy của khối chóp bằng bao nhiêu để thể tích của nó là lớn nhất A.
3
2
2
d
m
B.
5
...
Đọc tiếp
Từ một tấm bìa hình vuông ABCD có cạnh bằng 5 dm, người ta cắt bỏ bốn tam giác bằng nhau là AMB, BNC, CPD, DQA. Với phần còn lại, người ta gấp lên và ghép lại để thành hình chóp tứ giác đều. Hỏi cạnh đáy của khối chóp bằng bao nhiêu để thể tích của nó là lớn nhất
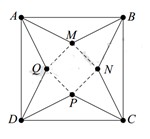
A. 3 2 2 d m
B. 5 2 d m
C. 2 2 d m
D. 5 2 2 d m
Từ một tấm bìa hình vuông ABCD có cạnh bằng 5 dm, người ta cắt bỏ bốn tam giác bằng nhau là AMB, BNC, CPD, DQA. Với phần còn lại, người ta gấp lên và ghép lại để thành hình chóp tứ giác đều. Hỏi cạnh đáy của khối chóp bằng bao nhiêu để thể tích của nó là lớn nhất A.
3
2
2
d
m
B.
5
2
d
m
C.
2...
Đọc tiếp
Từ một tấm bìa hình vuông ABCD có cạnh bằng 5 dm, người ta cắt bỏ bốn tam giác bằng nhau là AMB, BNC, CPD, DQA. Với phần còn lại, người ta gấp lên và ghép lại để thành hình chóp tứ giác đều. Hỏi cạnh đáy của khối chóp bằng bao nhiêu để thể tích của nó là lớn nhất
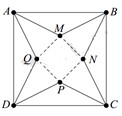
A. 3 2 2 d m
B. 5 2 d m
C. 2 2 d m
D. 5 2 2 d m