1) a,b là âm hay dương:
a) ab < a , a > 0
b) -ab > a , b < 0
c) -ab > 0 ; a > 0
d) a(-b) < a , b > 0
Những câu hỏi liên quan
a : \(\dfrac{y}{x}.\sqrt{\dfrac{x^2}{y^4}}\) với y ≥ 0 , y ≠ 0
b : \(\dfrac{5}{2}x^3y^3.\sqrt{\dfrac{16}{x^4y^8}}\)với x,y ≠ 0
c : \(ab^2\sqrt{\dfrac{3}{a^2b^4}}\)với a ≥ 0 , b ≠ 0
a) \(\dfrac{y}{x}\cdot\sqrt{\dfrac{x^2}{y^4}}\)
\(=\dfrac{y}{x}\cdot\dfrac{\sqrt{x^2}}{\sqrt{\left(y^2\right)^2}}\)
\(=\dfrac{y}{x}\cdot\dfrac{x}{y^2}\)
\(=\dfrac{1}{y}\)
b) \(\dfrac{5}{2}x^3y^3\cdot\sqrt{\dfrac{16}{x^4y^8}}\)
\(=\dfrac{5}{2}x^3y^3\cdot\dfrac{\sqrt{16}}{\sqrt{\left(x^2y^4\right)^2}}\)
\(=\dfrac{5}{2}x^3y^3\cdot\dfrac{4}{x^2y^4}\)
\(=\dfrac{20x^3y^3}{2x^2y^4}\)
\(=\dfrac{10x}{y}\)
c) \(ab^2\sqrt{\dfrac{3}{a^2b^4}}\)
\(=ab^2\dfrac{\sqrt{3}}{\sqrt{\left(ab^2\right)^2}}\)
\(=ab^2\cdot\dfrac{\sqrt{3}}{ab^2}\)
\(=\sqrt{3}\)
Đúng 2
Bình luận (0)
\(a,\dfrac{y}{x}\cdot\sqrt{\dfrac{x^2}{y^4}}\left(y\ge0;x,y\ne0\right)\) (sửa đề)
\(=\dfrac{y}{x}\cdot\dfrac{\sqrt{x^2}}{\sqrt{y^4}}\)
\(=\dfrac{y}{x}\cdot\dfrac{x}{\sqrt{\left(y^2\right)^2}}\)
\(=\dfrac{y}{x}\cdot\dfrac{x}{y^2}\)
\(=\dfrac{1}{y}\)
\(---\)
\(b,\dfrac{5}{2}x^3y^3\cdot\sqrt{\dfrac{16}{x^4y^8}}\left(x,y\ne0\right)\)
\(=\dfrac{5}{2}x^3y^3\cdot\dfrac{\sqrt{16}}{\sqrt{x^4y^8}}\)
\(=\dfrac{5x^3y^3}{2}\cdot\dfrac{4}{x^2y^4}\)
\(=\dfrac{5x\cdot2}{y}\)
\(=\dfrac{10x}{y}\)
\(---\)
\(c,ab^2\sqrt{\dfrac{3}{a^2b^4}}\left(a>0;b\ne0\right)\) (sửa đề)
\(=ab^2\cdot\dfrac{\sqrt{3}}{\sqrt{a^2b^4}}\)
\(=\dfrac{ab^2\sqrt{3}}{\sqrt{\left(ab^2\right)^2}}\)
\(=\dfrac{ab^2\sqrt{3}}{ab^2}\)
\(=\sqrt{3}\)
#\(Toru\)
Đúng 0
Bình luận (0)
1 Tìm số nguyên n sao cho
a (-2019) (n+1)<0
b 2020 (n-1)>0
2 Cho a là một số nguyên dương Hỏi b là số nguyên dương hay âm nếu
1/ ab là một số nguyên dương
2/ ab là một số nguyên âm
cho a,b hai số nguyên âm khẳng định nào sau đây đúng?
A. a.b>0
B. a.b<0
C. a+b>0
D. a+b∈ N
A
Hai số nguyên âm nhân với nhau luôn lớn hơn hoặc bằng 0
Đúng 2
Bình luận (0)
15.Cho a là một số nguyên dương. Hỏi b là số nguyên dương hay âm nếu :
a) ab là một số nguyên dương ;
b) ab là một số nguyên âm.
Cho a là một số nguyên dương. Hỏi b là số nguyên dương hay âm nếu :
a) ab là một số nguyên dương
=> b là một số nguyên dương.
b) ab là một số nguyên âm.
=> b là một số nguyên âm
Cho a là một số nguyên dương .Hỏi b là số nguyên dương hay âm nếu : a) ab là một số nguyên dương ; b) ab là một số nguyên âm
a) Nếu a là số nguyên dương thì b là số nguyên dương.
b) Nếu a là số nguyên dương thì b là số nguyên âm.
Cho a là số nguyên dương. Hỏi b là số nguyên âm hay số nguyên dương
a)ab là số nguyên dương
b)ab là số nguyên âm
a) a là một số nguyên dương. Tích a.b là một số nguyên dương
Suy ra b là một số nguyên dương
b) a là một số nguyên dương. Tích a.b là một số nguyên âm
Suy ra b là một số nguyên âm
a) b là số nguyên dương
b) b là số nguyên âm
lim
x
→
0
(
x
2
+
2012
)
1
-
2
x
7
-
2012...
Đọc tiếp
lim x → 0 ( x 2 + 2012 ) 1 - 2 x 7 - 2012 x = a b với a b là phân số tối giản, a là số nguyên âm. Tổng a+b bằng
A.-4017.
B. -4018.
C. -4015.
D. -4016.
Chọn A
*Ta có:
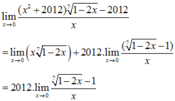
* Xét hàm số 
ta có 
.
Theo định nghĩa đạo hàm ta có:
Đúng 0
Bình luận (0)
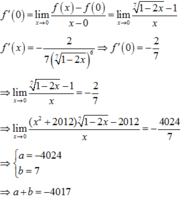
Phương trình ax+b=0 là phương trình bậc nhất một ẩn khi:
a/ a > 0
b/ a < 0
c/ a = 0
d/ a ≠ 0
Ptr `ax + b = 0` là ptr bậc nhất `1` ẩn `<=> a \ne 0`
`-> D`
Đúng 2
Bình luận (23)
Xem thêm câu trả lời
Rút gọn các biểu thức sau:
a
)
a
b
+
a
b
+
a
b
b
a
v
ớ
i
0
v
à b0
b
b
)
$
m
1
−
2
x
+
x
2...
Đọc tiếp
Rút gọn các biểu thức sau:
a ) a b + a b + a b b a v ớ i > 0 v à b>0 b > b ) $ m 1 − 2 x + x 2 ⋅ 4 m − 8 m x + 4 m x 2 81 v ớ i m > 0 v à x ≠ 1
