a.

Trong tam giác vuông ABC:

\(tan\widehat{ACB}=\dfrac{AB}{AC}\Rightarrow AC=AB.tan\widehat{ACB}=30.tan30^0=10\sqrt{3}\left(cm\right)\)

Áp dụng định lý Pitago:

\(BC=\sqrt{AB^2+AC^2}=20\sqrt{3}\left(cm\right)\)

\(\widehat{ABC}=90^0-\widehat{ACB}=60^0\)

b.

Áp dụng định lý Pitago:

\(BC=\sqrt{AB^2+AC^2}=\sqrt{569}\left(cm\right)\)

\(tan\widehat{ABC}=\dfrac{AC}{AB}=\dfrac{13}{20}\Rightarrow\widehat{ABC}\approx33^0\)

\(\widehat{ACB}=90^0-\widehat{ABC}=57^0\)

ΔABC vuông tại A

=>góc B+góc C=90 độ

=>góc C=60 độ

Xét ΔABC vuông tại A có \(cosB=\dfrac{AB}{BC}\)

=>8/BC=căn 3/2

=>BC=16/căn 3(cm)

=>\(AC=\dfrac{8}{\sqrt{3}}\left(cm\right)\)

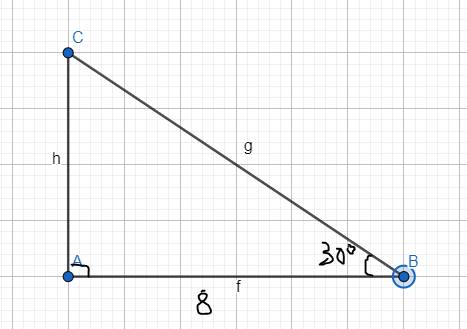
\(\widehat{C}=90^0-\widehat{B}=90^0-30^0=60^0\)

\(sin60=\dfrac{AB}{BC}=\dfrac{8}{BC}\Rightarrow BC=9,2\left(cm\right)\\ \sin30=\dfrac{AC}{BC}=\dfrac{AC}{9,2}\\ \Rightarrow AC=4,6\left(cm\right)\)

Xét ΔAHB vuông tại H có 

\(AB=\dfrac{AH}{\sin30^0}=6:\dfrac{1}{2}=12\left(cm\right)\)

\(\Leftrightarrow AC=12\sqrt{3}\left(cm\right)\)

\(\Leftrightarrow BC=24\sqrt{3}\left(cm\right)\)

a, tam giác ABC vuông tại B có góc A = 30 độ => AC = 2 BC = 2. 3 = 6 cm

theo định lí Pytago ta có AB = \(\sqrt{ÃC^2-BC^2}=\sqrt{6^2-3^2}\) = \(3\sqrt{3}\) cm

góc C = 90 - 30 = 60 độ

b, tam giác ABH vuông tại H có góc A = 30 độ => AB = 2 BH => BH = \(\frac{3\sqrt{3}}{2}\)cm

theo định lí Pytago ta có AH = \(\sqrt{AB^2-BH^2}=\sqrt{\left(3\sqrt{3}\right)^2-\left(\frac{3\sqrt{3}}{2}\right)^2}=4,5cm\)

diện tích tam giác ABH =\(\frac{1}{2}.BH.AH=\frac{1}{2}.\frac{3\sqrt{3}}{2}.4,5=\frac{27\sqrt{3}}{8}\)cm vuông

mk bận quá k lm kịp 2 câu còn lại thông cảm nha 

BC>AC>AB

c = 60

BC > AB > AC

Xét ΔABC có \(\widehat{B}< \widehat{C}< \widehat{A}\)

nên AC<AB<BC