Cho tứ diện ABCD. Gọi G 1 , G 2 , G 3 lần lượt là trọng tâm các tam giác ABC, ACD, ABD. Chứng minh rằng ( G 1 G 2 G 3 ) / / ( B C D ) .

Những câu hỏi liên quan
Cho hình tứ diện đều ABCD có cạnh bằng 3. Gọi G₁, G₂, G₃, G₄ lần lượt là trọng tâm của bốn mặt của tứ diện ABCD. Tính thể tích V của khối tứ diện G₁G₂G₃G₄. A.
2
4
B.
2
18
C.
9
2
32
D.
2
12
Đọc tiếp
Cho hình tứ diện đều ABCD có cạnh bằng 3. Gọi G₁, G₂, G₃, G₄ lần lượt là trọng tâm của bốn mặt của tứ diện ABCD. Tính thể tích V của khối tứ diện G₁G₂G₃G₄.
A. 2 4
B. 2 18
C. 9 2 32
D. 2 12
Chọn D
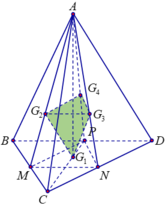
Tứ diện đều ABCD ⇒ A G 1 ⊥ B C D
Ta có ngay 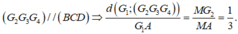
Cạnh C G 1 = B C 3 = 3 ⇒ G 1 A = A C 2 - G 1 C 2 = 6 ⇒ d G 1 ; G 2 G 3 G 4 = 6 3
Lại có G 2 G 3 M N = A G 2 A M = 2 3 ⇒ G 2 G 3 = 2 3 M N = 1 3 B D = 1
Tương tự G₃G₄=1, G₄G₂=1 ⇒ ∆ G 2 G 3 G 3 là tam giác đều có cạnh bằng 1
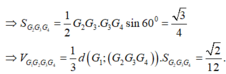
Đúng 0
Bình luận (0)
Cho tứ diện đều ABCD có cạnh a. Gọi G, G’ lần lượt là trọng tâm của tam giác ABC và ABD. Diện tích của thiết diện của hình tứ diện khi cắt bởi mặt phẳng (BGG’) là: A. B. C. D.
Đọc tiếp
Cho tứ diện đều ABCD có cạnh a. Gọi G, G’ lần lượt là trọng tâm của tam giác ABC và ABD. Diện tích của thiết diện của hình tứ diện khi cắt bởi mặt phẳng (BGG’) là:
A. ![]()
B. ![]()
C. ![]()
D. 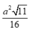
Đáp án D
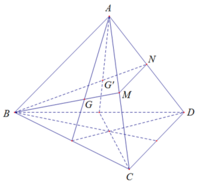
Trong(ABC), ta có: BG cắt AC tại M
Trong (ABD), ta có: BG’ cắt AD tại N
⇒ (BGG’) ∩ (ACD) = MN
Thiết diện cần tìm là (BMN)
Xét tam giác BMN có:
MN = 1 2 CD = a 2 ( MN là đường trung bình của tam giác ACD)
BM = BN = a 3 2 (BM, BN lần lượt là đường trung tuyến của tam giác ABC, ABD)
Áp dụng công thức heron:
S = p p - a p - b p - c = a 2 11 6
Đúng 0
Bình luận (0)
Cho tứ diện ABCD. Gọi G là trọng tâm của ΔBCD. Hai điểm M và N lần lượt thuộc cạnh BC,CD sao cho \(\dfrac{BM}{BC}=\dfrac{1}{4};\dfrac{NC}{ND}=\dfrac{3}{2}\). Chứng minh A,M,N,G đồng phẳng
1.` Cho tứ diện ABCD. Gọi G là trọng tâm tam giác BCD. Tìm điểm M xác định bởi đẳng thức vectơ .overrightarrow{AM}overrightarrow{AB}+overrightarrow{AC}+overrightarrow{AD}.2.Gọi ,MN lần lượt là trung điểm của các cạnh ACvà BDcủa tứdiện .ABCD Gọi I là trung điểm của đoạn MN. Tìm giá trị thực của k thỏa mãn đẳng thức vectơ overrightarrow{IA}+2k-1overrightarrow{IB}+koverrightarrow{IC}+overrightarrow{ID}overrightarrow{0}
Đọc tiếp
1.` Cho tứ diện ABCD. Gọi G là trọng tâm tam giác BCD. Tìm điểm M xác định bởi đẳng thức vectơ .\(\overrightarrow{AM}=\overrightarrow{AB}+\overrightarrow{AC}+\overrightarrow{AD}\).
2.
Gọi ,MN lần lượt là trung điểm của các cạnh ACvà BDcủa tứdiện .ABCD Gọi I là trung điểm của đoạn MN. Tìm giá trị thực của k thỏa mãn đẳng thức vectơ \(\overrightarrow{IA}+2k-1\overrightarrow{IB}+k\overrightarrow{IC}+\overrightarrow{ID}=\overrightarrow{0}\)
1/ \(\overrightarrow{AM}=3\overrightarrow{AM}+\overrightarrow{MB}+\overrightarrow{MC}+\overrightarrow{MD}\)
\(\Leftrightarrow2\overrightarrow{AM}+3\overrightarrow{MG}=\overrightarrow{0}\)
\(\Leftrightarrow2\overrightarrow{AM}+3\overrightarrow{MA}+3\overrightarrow{AG}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{AM}=3\overrightarrow{AG}\)
Ban tu ket luan
2/ Bạn coi lại đề bài, đẳng thức kia có vấn đề. 2k-1IB??
Đúng 1
Bình luận (2)
Cho khối tứ diện ABCD có thể tích là V. Gọi E, F, G lần lượt là trung điểm BC, BD, CD và M, N, P, Q lần lượt là trọng tâm
∆
A
B
C
;
∆
A
B
D
;
∆
A
C
D
;
∆
B
C
D
. Tính thể tích khối tứ diện MNPQ theo V. A.
V
9
B.
V
3
C. ...
Đọc tiếp
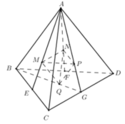
Cho khối tứ diện ABCD có thể tích là V. Gọi E, F, G lần lượt là trung điểm BC, BD, CD và M, N, P, Q lần lượt là trọng tâm ∆ A B C ; ∆ A B D ; ∆ A C D ; ∆ B C D . Tính thể tích khối tứ diện MNPQ theo V.
A. V 9
B. V 3
C. 2 V 9
D. V 27
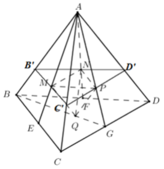
Ta có:
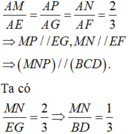
Ta có ∆ M N P đồng dạng với ∆ B C D theo tỉ số
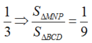
Dựng B ' C ' qua M và song song BC. C ' D ' qua P và song song với CD.
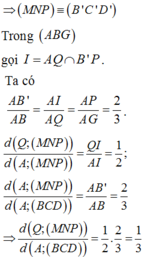

Chọn D.
Đúng 1
Bình luận (0)
Cho tứ diện đều ABCD cạnh a. gọi E, F, G lần lượt trung điểm BC, AC, AD. xác định thiết diện của tứ diện với mặt phẳng (EFG). tính diện tích thiết diện??
FG là đường trung bình tam giác (ACD) nên FG//CD
Gọi H là trung điểm của BD => EH là đường trung bình tam giác BCD
\(\Rightarrow EH//CD\Rightarrow H\in\left(EFG\right)\)
\(\Rightarrow EFGH\) là tiết diện của tứ diện và (EFG)
Ta có: \(\left\{{}\begin{matrix}EF=GH=\frac{1}{2}AB=\frac{a}{2}\\FG=EH=\frac{1}{2}CD=\frac{a}{2}\end{matrix}\right.\) (t/c đường trung bình)
\(\Rightarrow EFGH\) là hình thoi
Mặt khác do tính chất của tứ diện đều nên \(EG=HF\)
\(\Rightarrow EFGH\) là hình vuông
Diện tích tiết diện: \(EF^2=\frac{a^2}{4}\)
Đúng 0
Bình luận (0)
Cho tứ diện ABCD Gọi G,E lần lượt là trọng tâm của tam giác
A
B
D
v
à
A
B
C
.
Mệnh đề nào dưới đây đúng: A.
G
E
v
à
CD
chéo nhau B.
G
E
/
/
C
D
C. GE và AD D. GE cắt CD
Đọc tiếp
Cho tứ diện ABCD Gọi G,E lần lượt là trọng tâm của tam giác A B D v à A B C . Mệnh đề nào dưới đây đúng:
A. G E v à CD chéo nhau
B. G E / / C D
C. GE và AD
D. GE cắt CD
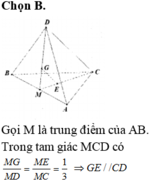
Chọn B.
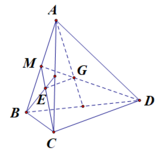
Gọi M là trung điểm của AB .
Có G là trọng tâm tam giác ABC nên G M D M = 1 3
Và E là trọng tâm tam giác ABC nên E M C M = 1 3
Áp dụng định lý Ta – lét có : G E // D C .
Đúng 0
Bình luận (0)
Cho tứ diện ABCD. Gọi G và E lần lượt là trọng tâm của tam giác ABD và ABC. Mệnh đề nào dưới đây là đúng? A. GE và CD chéo nhau B. GE//CD C. GE cắt AD D. GE cắt CD
Đọc tiếp
Cho tứ diện ABCD. Gọi G và E lần lượt là trọng tâm của tam giác ABD và ABC. Mệnh đề nào dưới đây là đúng?
A. GE và CD chéo nhau
B. GE//CD
C. GE cắt AD
D. GE cắt CD
Cho tứ diện ABCD. Gọi G và E lần lượt là trọng tâm của tam giác ABD và ABC. Mệnh đề nào dưới đây đúng:
A. GE//CD
B. GE và CD chéo nhau
C. GE cắt AD
D. GE cắt CD
Đáp án A
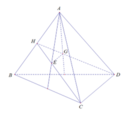
Xét tam giác HCD có:
![]()
⇒ EG // CD
Đúng 0
Bình luận (0)
Cho tứ giác ABCD có hai đường chéo vuông góc với nhau. Gọi E, F, G, H lần lượt là trung điểm các cạnh AB, BC, CD, DA. Biết diện tích của tứ giác ABCD là
18
m
2
thì diện tích của tứ giác EFGH là: A.
9
m
2
B.
5
m
2
C.
6
m
2
D.
7...
Đọc tiếp
Cho tứ giác ABCD có hai đường chéo vuông góc với nhau. Gọi E, F, G, H lần lượt là trung điểm các cạnh AB, BC, CD, DA. Biết diện tích của tứ giác ABCD là 18 m 2 thì diện tích của tứ giác EFGH là:
A. 9 m 2
B. 5 m 2
C. 6 m 2
D. 7 , 5 m 2
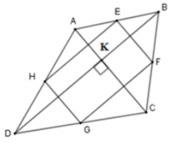
Vì E, F, G, H lần lượt là trung điểm các cạnh AB,BC,CD,DA nên EF, FG, GH, HE lần lượt là đường trung bình của tam giác ABC, BCD, ADC, ADB nên
EF//HG (cùng song song với AC)
HE//FG (cùng song song với BD)
Suy ra tứ giác EFGH là hình bình hành
Mà A C ⊥ B D (gt) ⇒ E F ⊥ F G
Suy ra EFGH là hình chữ nhật
Do đó S E F G H = H E . E F mà E F = 1 2 A C ; H E = 1 2 B D (tính chất đường trung bình)

Đúng 0
Bình luận (0)