hoc gioi the hihiihihihhhihihihihiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiii

,mnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnn

Mình không biết sin lỗi vạn

Ta thấy x= 1 không là nghiệm của bất phương trình đã cho nhưng x= 1 là nghiệm của bất phương trình 4(x -1)+ 1> 2x(x-1) – 1.

Do đó, hai bất phương  trình này không tương đương với nhau.

Chọn C.

Đáp án: D

x + 1 ( x - 2 ) 2 < x + 1

ĐKXĐ: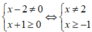 

Vậy tập xác định của bất phương trình là: [-1;2) ∪ (2; + ∞ )

Chú ý: Học sinh thường hay nhầm lẫn giữa đáp án C và D. Khi câu hỏi là “tập xác định” thì chúng ta phải biểu diễn kết quả dưới dạng tập hợp như đáp án D

Với m = 1/2 thì bpt (1) \(\Leftrightarrow\left(x-\dfrac{1}{2}\right)^2\le0\Leftrightarrow x=\dfrac{1}{2}\)

bpt(2) \(\sqrt{\sqrt{x-1}+4}-\sqrt{\sqrt{x-1}+1}\ge1\) ( ĐK : \(x\ge1\) )

\(\Leftrightarrow\sqrt{\sqrt{x-1}+4}\ge1+\sqrt{\sqrt{x-1}+1}\) 

\(\Leftrightarrow\sqrt{x-1}+4\ge1+\sqrt{x-1}+1+2\sqrt{\sqrt{x-1}+1}\)

\(\Leftrightarrow2\ge2\sqrt{\sqrt{x-1}+1}\Leftrightarrow1\ge\sqrt{\sqrt{x-1}+1}\)  \(\Leftrightarrow\sqrt{x-1}+1\le1\Leftrightarrow\sqrt{x-1}\le0\Leftrightarrow x=1\) 

bpt (2) có no x = 1 . Loại A 

Với m khác 1/2 \(x^2-x+m\left(1-m\right)\le0\)

\(\Leftrightarrow x^2-m^2-\left(x-m\right)\le0\)  \(\Leftrightarrow\left(x-m\right)\left(x+m-1\right)\le0\)

\(\Leftrightarrow\left[{}\begin{matrix}x\ge m;x\le1-m\\x\le m;x\ge1-m\end{matrix}\right.\)

Vì bpt (1) là hệ quả bpt (2) nên bpt (1) có no x = 1 

Khi đó : \(\left[{}\begin{matrix}1\ge m;1\le1-m\\1\le m;1\ge1-m\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m\le0\\m\ge1\end{matrix}\right.\)

Chọn B 

Tìm tất cả tham số mm để bất phương trình x2−x+m(1−m)≤0x2-x+m(1-m)≤0 là hệ quả của bất phương trình √√x−1+4−√√x−1+1≥1x-1+4-x-1+1≥1?
A.m=12A.m=12
B.m≤0B.m≤0 hoặc m≥1m≥1
C.m≥1C.m≥1
D.m≤0D.m≤0

3:

x^2-2x+1-m^2<=0

=>(x-1)^2-m^2<=0

=>(x-1)^2<=m^2

=>-m<=x-1<=m

=>-m+1<=x<=m+1

mà x thuộc [-1;2]

nên -m+1>=-1 và m+1<=2

=>-m>=-2 và m<=1

=>m<=2 và m<=1

=>m<=1

\(\left|x-5\right|=2x\)ĐK : x>=0 

TH1 : x - 5 = 2x <=> x = -5 ( loại )

TH2 : x - 5 = -2x <=> 3x = 5 <=> x = 5/3 ( tm )

Vậy tập nghiệm pt là S = { 5/3 } 

\(\left(x-2\right)^2+2\left(x-1\right)\le x^2+4\)

\(\Leftrightarrow x^2-4x+4+2x-2-x^2-4\le0\)

\(\Leftrightarrow-2x-2\le0\Leftrightarrow x+1\ge0\Leftrightarrow x\ge-1\)

Vậy tập nghiệm bft là S = { x | x > = -1 } 

Ta có: \(\left|x-5\right|=2x\)

\(\Leftrightarrow\left[{}\begin{matrix}x-5=2x\left(x\ge5\right)\\x-5=-2x\left(x< 5\right)\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x-2x=5\\x+2x=5\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}-x=5\\3x=5\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-5\left(loại\right)\\x=\dfrac{5}{3}\left(nhận\right)\end{matrix}\right.\)

Ta có: 2x + 1 > 2(x + 1)

      ⇔ 2x + 1 > 2x + 2

      ⇔ 0x > 1

Vậy bất phương trình vô nghiệm.

1. \(\left|\frac{2x^2-x}{3x-4}\right|\ge1\) Điều kiện: \(x\ne\frac{4}{3}\)

\(\Leftrightarrow\orbr{\begin{cases}\frac{2x^2-x}{3x-4}\ge1\\\frac{2x^2-x}{3x-4}\le-1\end{cases}}\Leftrightarrow\orbr{\begin{cases}\frac{x^2-2x+2}{3x-4}\ge0\\\frac{x^2+x-2}{3x-4}\le0\end{cases}}\)

\(\Leftrightarrow\orbr{\begin{cases}x>\frac{4}{3}\\x\in(-\infty;-2]U[1;\frac{4}{3})\end{cases}}\Leftrightarrow x\in(-\infty;-2]U[1;+\infty)\backslash\left\{\frac{4}{3}\right\}\)

2.\(\hept{\begin{cases}x^2\le-2x+3\left(1\right)\\\left(m+1\right)x\ge2m-1\left(2\right)\end{cases}}\)

\(\left(1\right)\Leftrightarrow x^2+2x-3\le0\Leftrightarrow-3\le x\le1\)

+) Nếu \(m=-1\) thì (2) vô nghiệm, suy ra \(m\ne-1\)

+) Nếu \(m>-1\) thì \(\left(2\right)\Leftrightarrow x\ge\frac{2m-1}{m+1}\)

Hệ BPT có nghiệm duy nhất \(\Leftrightarrow\frac{2m-1}{m+1}=1\Leftrightarrow m=2>-1\)

+) Nếu \(m< -1\)thì \(\left(2\right)\Leftrightarrow x\le\frac{2m-1}{m+1}\)

Hệ BPT có nghiệm duy nhất \(\Leftrightarrow\frac{2m-1}{m+1}=-3\Leftrightarrow m=-\frac{2}{5}< -1\)

Vậy \(m=\left\{\frac{-2}{5};2\right\}\)

1. |2x2−x3x−4 |≥1 Điều kiện: x≠43 

⇔[

⇔[

⇔[

⇔x∈(−∞;−2]U[1;+∞)\{43 }

2.{

(1)⇔x2+2x−3≤0⇔−3≤x≤1

∣∣∣∣∣​3x−42x2−x​∣∣∣∣∣​≥1⇔⎣⎢⎢⎢⎡​​3x−42x2−x​≥13x−42x2−x​≤−1​⇔⎣⎢⎢⎢⎡​​3x−42x2−4x+4​≥03x−42x2+2x−4​≤0​⇔⎣⎢⎢⎡​​3x−4>03x−42x2+2x−4​≤0​

\Leftrightarrow \left[\begin{aligned}&{x>\dfrac{4}{3} } \\ &{1\le x<\dfrac{4}{3} } \\ &{x\le -2} \end{aligned}\right.⇔⎣⎢⎢⎢⎢⎢⎡​​x>34​1≤x<34​x≤−2​ .

Tập nghiệm :S=\left(-\infty ;-2\right]\cup \left[1;\dfrac{4}{3} \right)\cup \left(\dfrac{4}{3} ;+\infty \right)S=(−∞;−2]∪[1;34​)∪(34​;+∞).

2.

Ta có: \left\{\begin{aligned}&{x^{2} \le -2x+3} \\ &{\left(m+1\right)x\ge 2m-1} \end{aligned}\right. \Leftrightarrow \left\{\begin{aligned}&{x^{2} +2x-3\le 0} \\ &{\left(m+1\right)x\ge 2m-1} \end{aligned}\right. \Leftrightarrow \left\{\begin{aligned}&{-3\le x\le 1} \\ &{\left(m+1\right)x\ge 2m-1} \end{aligned}\right.{​x2≤−2x+3(m+1)x≥2m−1​⇔{​x2+2x−3≤0(m+1)x≥2m−1​⇔{​−3≤x≤1(m+1)x≥2m−1​.

+ Trường hợp 1: $m=-1$

Hệ BPT trở thành: \left\{\begin{aligned}& {-3\le x\le 1} \\ &{0\ge -3} \end{aligned}\right.{​−3≤x≤10≥−3​. Hệ luôn đúng với $\forall x\in \left[-3;1\right]$.

Vậy $m=-1$ loại.

+ Trường hợp 2: $m>-1$

Hệ BPT trở thành: \left\{\begin{aligned}& {-3\le x\le 1} \\ &{x\ge \dfrac{2m-1}{m+1} } \end{aligned}\right.⎩⎪⎨⎪⎧​​−3≤x≤1x≥m+12m−1​​.

Hệ có nghiệm duy nhất khi \dfrac{2m-1}{m+1} =1\Leftrightarrow 2m-1=m+1\Leftrightarrow m=2m+12m−1​=1⇔2m−1=m+1⇔m=2 (nhận).

+ Trường hợp 3: $m<-1$ Hệ BPT trở thành: \left\{\begin{aligned}& {-3\le x\le 1} \\ &{x\le \dfrac{2m-1}{m+1} } \end{aligned}\right.⎩⎪⎨⎪⎧​​−3≤x≤1x≤m+12m−1​​.

Hệ có nghiệm duy nhất khi \dfrac{2m-1}{m+1} =-3\Leftrightarrow 2m-1=-3m-3\Leftrightarrow m=\dfrac{-2}{5}m+12m−1​=−3⇔2m−1=−3m−3⇔m=5−2​ (loại). Vậy $m=2$ hệ có nghiệm duy nhất.