Tìm số giao điểm của đồ thị hàm số y x4 – 2x2 và đồ thị hàm số y x2 – 2 A. 4 B. 2 C. 3 D. 1
Đọc tiếp
Tìm số giao điểm của đồ thị hàm số y = x4 – 2x2 và đồ thị hàm số y = x2 – 2
A. 4
B. 2
C. 3
D. 1
Những câu hỏi liên quan
Tìm số giao điểm của đồ thị hàm số y x4 – 2x2 và đồ thị hàm số y x2 – 2 A. 4 B. 2. C. 3 D. 1
Đọc tiếp
Tìm số giao điểm của đồ thị hàm số y = x4 – 2x2 và đồ thị hàm số y = x2 – 2
A. 4
B. 2.
C. 3
D. 1
Đáp án A.
Phương trình hoành độ giao điểm là
x4 – 2x2 = x2 – 2 <=> x4 – 3x2 + 2 = 0
Vậy có 4 giao điểm của hai đồ thị.
Đúng 0
Bình luận (0)
Cho hàm số y = x 4 - 2 x 2 - 2 có đồ thị (C) và đồ thị ( P ) : y = 1 - x 2 . Số giao điểm của (P) và đồ thị (C) là:
A. 1
B. 4
C. 2
D. 3
Cho hàm số y x4 – 4x2 – 2 có đồ thị (C) và đồ thị (P) : y 1- x2. Số giao điểm của (P) và đồ thị (C) là A. 2 B. 1 C. 3 D. 4
Đọc tiếp
Cho hàm số y = x4 – 4x2 – 2 có đồ thị (C) và đồ thị (P) : y = 1- x2. Số giao điểm của (P) và đồ thị (C) là
A. 2
B. 1
C. 3
D. 4
Đáp án A.
Phương trình hoành độ giao điểm:
x4 – 4x2 – 2 = 1 – x2 ⇔ x4 – 3x2 – 3 = 0
Đúng 0
Bình luận (0)
Cho hàm số
y
x
4
-
4
x
2
-
2
có đồ thị (C) và đồ thị
P
:
y
1
-
x
2
.
Số giao điểm của (P) và đồ thị (C) là A. 1. B. 4. C. 2. D. 3.
Đọc tiếp
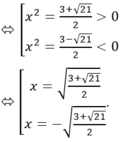
Cho hàm số y = x 4 - 4 x 2 - 2 có đồ thị (C) và đồ thị P : y = 1 - x 2 . Số giao điểm của (P) và đồ thị (C) là
A. 1.
B. 4.
C. 2.
D. 3.
Gọi M và N là giao điểm của đồ thị hai hàm số y = x 4 − 2 x 2 + 2 v à y = − x 2 + 4 . Tọa độ trung điểm I của đoạn thẳng MN là
A. (1;0)
B. (0;2)
C. (2;0)
D. (0;1)
Chọn B.
Phương pháp:
Giải phương trình hoành độ giao điểm của hai đồ thị hàm số. Tìm tọa độ giao điểm M và N. Tìm tọa độ trung điểm I của MN.
Cách giải:
Phương trình hoành độ giao điểm của đồ thị hai hàm số
Đúng 0
Bình luận (0)
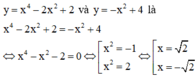
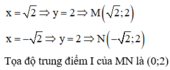
Gọi M và N là giao điểm của đồ thị hai hàm số y = x 4 - 2 x 2 + 2 và y = - x 2 + 4 . Tọa độ trung điểm I của đoạn thẳng MN là
A. (1;0)
B. (0;2)
C. (2;0)
D. (0;1)
Cho hàm số y x4 – 2x2 – 1. Tìm số giao điểm của đồ thị hàm số với trục Ox: A. 1. B. 3 C. 4 D. 2
Đọc tiếp
Cho hàm số y = x4 – 2x2 – 1. Tìm số giao điểm của đồ thị hàm số với trục Ox:
A. 1.
B. 3
C. 4
D. 2
Đáp án D.
Xét phương trình y = 0
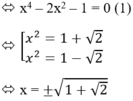
Phương trình (1) có hai nghiệm => số giao điểm của đồ thị với trục Ox là 2
Đúng 0
Bình luận (0)
Tìm số giao điểm n của đồ thị hai hàm số sau:
y
x
4
−
3
x
2
+
2
và
y
x
2
−
2
A. n 2 B. n 0 C. n 4 D. n 1
Đọc tiếp
Tìm số giao điểm n của đồ thị hai hàm số sau: y = x 4 − 3 x 2 + 2 và y = x 2 − 2
A. n = 2
B. n = 0
C. n = 4
D. n = 1
Đáp án A.
Xét phương trình
x 4 − 3 x 2 + 2 = x 2 − 2 ⇔ x 4 − 4 x 2 + 4 = 0 ⇔ x 2 = 2 ⇔ x = 2 x = − 2 .
Vậy ta có 2 giao điểm.
Đúng 0
Bình luận (0)
Câu 7: (1,0 điểm) Cho hàm số y = 2x2 (P) và hàm số y = -4x - 2 (d) a) Vẽ đồ thị hàm số y = 2x2 b) Tìm tọa độ giao điểm của Parabol (P) và đường thẳng (d) bằng phương pháp đại số.
làm bài này đâu nhất thiết phải dùng cách nào đâu bạn, vận dụng cách khoa học nhất là đc rồi nhé
a, bạn tự vẽ
b, Theo bài ra ta có hệ
\(\left\{{}\begin{matrix}2x^2+4x+2=0\\y=2x^2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x^2+4x+2=0\\y=2x^2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left(x+1\right)^2=0\\y=2x^2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-1\\y=2\end{matrix}\right.\)
Vậy (P) cắt (d) tại A(-1;2)
Đúng 0
Bình luận (0)