Cho hình vẽ, đường tròn tâm O trên có đường kính là:
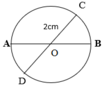
A. AB, CO
B. AB, CD
C. AO, CD
D. BO, CD
Những câu hỏi liên quan
Cho nửa đường tròn đường kính AB, tâm O. Đường tròn tâm A bán kính AO cắt nửa đường tròn đã cho tại C. Đường tròn tâm B bán kính BO cắt nửa đường tròn đã cho tại D. Đường thẳng qua O và song song với AD cắt nửa đường tròn đã cho tại E. Chứng minh CD song song với AB.
∆ ACB nội tiếp trong đường tròn (O) có AB là đường kính nên ∆ ABC vuông tại C
CO = OA = (1/2)AB (tính chất tam giác vuông)
AC = AO (bán kính đường tròn (A))
Suy ra: AC = AO = OC
∆ ACO đều góc AOC = 60 °
∆ ADB nội tiếp trong đường tròn đường kính AB nên ∆ ADB vuông tại D
DO = OB = OA = (1/2)AB (tính chất tam giác vuông)
BD = BO(bán kính đường tròn (B))
Suy ra: BO = OD = BD
∆ BOD đều
Đúng 0
Bình luận (0)
Cho nửa đường tròn đường kính AB, tâm O. Đường tròn tâm A bán kính AO cắt nửa đường tròn đã cho tại C. Đường tròn tâm B bán kính BO cắt nửa đường tròn đã cho tại D. Đường thẳng qua O và song song với AD cắt nửa đường tròn đã cho tại E. So sánh hai cung BE và CD.
cho hình vuông ABCD. Đường tròn đường kính CD và cung tròn tâm A bán kính AD cắt nhau tại M (M khác D)
a)CMR đường thẳng DM đi qua trung điểm I của BC
b)Gọi O là tâm đường tròn đường kính CD, gọi K là giao điểm của AO và DI. CMR DK.AI=2OD^2
c)Vẽ cung tròn BD có tâm C, trên cung BD lấy điểm F bất kỳ tia CF cắt đường tròn đường kính CD ở E. CM EF bằng khoảng cách từ F đến AD
Vẽ đường tròn tâm O, đường kính AD. Vẽ đường tròn tâm A, bán kính AO cắt đường tròn tâm O ở B và F. Vẽ đường tròn tâm D, bán kính DO cắt đường tròn tâm O ở C và E (B và C thuộc cùng một nửa mặt phẳng bờ AD). Dùng compa so sánh các dây AB, BC, CD, DE, EF và FA.
Đọc tiếp
Vẽ đường tròn tâm O, đường kính AD. Vẽ đường tròn tâm A, bán kính AO cắt đường tròn tâm O ở B và F. Vẽ đường tròn tâm D, bán kính DO cắt đường tròn tâm O ở C và E (B và C thuộc cùng một nửa mặt phẳng bờ AD). Dùng compa so sánh các dây AB, BC, CD, DE, EF và FA.
Xác định được AB = BC = CD = DE = EF = FA.
Đúng 0
Bình luận (0)
Vẽ đường tròn tâm O, đường kính AD. Vẽ đường tròn tâm A, bán kính AO cắt đường tròn tâm O ở B và F. Vẽ đường tròn tâm D, bán kính DO cắt đường tròn tâm O ở C và E (B và C thuộc cùng một nửa mặt phẳng bờ AD). Dùng compa so sánh các dây AB, BC, CD, DE, EF và FA.
Xác định được AB = BC = CD = DE = EF = FA.
Đúng 0
Bình luận (0)
Câu 4(3d)
Cho đường tròn tâm O, đường kính AB. Lấy điểm C trên đường tròn sao cho số đo c AC bằng 60°. Vẽ dây CD vuông góc với AB tại M, dây BC cắt đường tròn đường kí
BO tại điểm thứ hai là I
a) Chứng minh Ol//AC và ba điểm O:I;D thẳng hàng
b)Xác định vị trí tương đối của đường thẳng MI với đường tròn đường kính BO c) Gọi N là điểm nằm giữa O và D. Tia CN cắt đường thẳng AD tại K, đường thẳng cắt đường thẳng OK tại E. Chứng minh tứ giác AOED nội tiếp
Đọc tiếp
Câu 4(3d) Cho đường tròn tâm O, đường kính AB. Lấy điểm C trên đường tròn sao cho số đo c AC bằng 60°. Vẽ dây CD vuông góc với AB tại M, dây BC cắt đường tròn đường kí BO tại điểm thứ hai là I a) Chứng minh Ol//AC và ba điểm O:I;D thẳng hàng b)Xác định vị trí tương đối của đường thẳng MI với đường tròn đường kính BO c) Gọi N là điểm nằm giữa O và D. Tia CN cắt đường thẳng AD tại K, đường thẳng cắt đường thẳng OK tại E. Chứng minh tứ giác AOED nội tiếp
Cho tam giác ABC nhọn AB <AC , đường cao AH .M,N là hình chiếu của H trên AB,AC . MN cắt BC tại D . Trên nửa mp bờ BC chứa A vẽ nửa đường tròn đường kính CD . Qua B kẻ đường vuông góc với CD cắt nửa đường tròn tại E. Gọi O là tâm đường tròn ngoại tiếp tam giác MNE . Cm: OE vuông góc DE
cho nữa đường tròn đường kính mn tâm O. vẽ tiếp tiến mx ny ,trên mx lấy D , trên ny lấy C sao cho sao cho gốc COD =90 . gọi I là trung điểm CD . Chứng Minh :
a) Mn là tiếp tiến của đường tròn , đường kính Cd
b)chứng minh co là phân giác gốc NCD
c) Cd là tiếp tiến của đường tròn tâm O
cho hình vẽ, biết O là tâm đường tròn đường kính CD; ABOD, góc DOE42o .Số đo của góc BAO là: A B E O D C
Đọc tiếp
cho hình vẽ, biết O là tâm đường tròn đường kính CD; AB=OD, góc DOE=42o .Số đo của góc BAO là:
góc BAO=1/2(sđ cung ED-sđ cung BC)
=1/2(42 độ-sđ cung BC)
=21 độ-1/2*sđ cung BC
BA=OD=BD
=>ΔBAD cân tại B
=>góc BAO=góc BOA=sđcung BC
=>21 độ-1/2*sđ cung BC=sđ cung BC
=>sđ cung BC=14 độ
=>góc BAO=21-7=14 độ
Đúng 1
Bình luận (0)
Cho đường tròn tâm 0 đường kính AB. Vẽ dãy CD đi qua trung điểm I của
OA và vuông góc với OA.
a) Tính độ dài dây CD biết AB = 20 cm
b) Trên tia đối của tia AO, lấy điểm M sao cho AM = AO. Chứng minh MC là tiếp tuyến của
đường tròn (O).
c) Qua điểm I kẻ dãy EF song song với MC. Gọi H, K lần lượt là chân đường vuông góc kẻ từ
A, B đến EF. Chứng minh EH = FK.
b: Xét ΔMCO có
CA là đường trung tuyến
CA=OM/2
Do đó: ΔMCO vuông tại C
Đúng 1
Bình luận (1)