Cho tam giác ABC. Lấy D, E trên các cạnh AB, AC sao cho DE // BC và A D = 8 c m , D B = 6 c m , A E = 10 c m . Độ dài cạnh AC là:
A. 8cm
B. 10cm
C. 15cm
D. 17,5cm
Cho tam giác ABC có AB = 6, AC = 8, BC =10.
a/ Chứng minh tam giác ABC vuông
b/ Lấy điểm D trên cạnh AB sao cho BD = 2. Từ D kẻ DE // BC ( E thuộc AC). Tính DE, EC?
Gọi 1/4 số a là 0,25 . Ta có :
a . 3 - a . 0,25 = 147,07
a . (3 - 0,25) = 147,07 ( 1 số nhân 1 hiệu )
a . 2,75 = 147,07
a = 147,07 : 2,75
a = 53,48
mình nha
cho mik hỏi ké: cũng đề như thế tìm D để BD+EC=DE
cho tam giác ABC nhọn, AB<AC .Trên cạnh AB lấy điểm D(D khác A và B),trên cạnh AC lấy điểm E sao cho góc ADE = ACB
a) CM : tam giác ADE đồng dạng tam giác ACB
b)Gọi i là giao điểm của BC và DE. CM: IB.IC=ID.IE
c)Lấy M là trung điểm BC . CM \(\dfrac{AD.AB}{AE.AM}\) =2
a: Xet ΔADE và ΔACB có
góc ADE=góc ACB
góc DAE chung
=>ΔADE đồng dạng với ΔACB
b: Xét ΔIDB và ΔICE có
góc IDB=góc ICE
góc I chung
=>ΔIDB đồng dạng với ΔICE
=>ID/IC=IB/IE
=>ID*IE=IB*IC
Bài 6. Cho tam giác cân ABC có AB= AC. Trên cạnh AB và AC lấy tương ứng hai điểm D và E sao cho AD = AE. Gọi M là trung điểm của BC. Chứng minh:
a) BE=CD
b) DAMD = DAME
c) DE // BC
a, Xét ABE và ACD có :
AB = AC(gt)
^A - chung
AE = AD (gt)
=> ABE = ACD (c.g.c)
=> BE=CD ( 2 cạnh tương ứng)
b,vì tam giác MBD= tam giác MEC:
=> DM=EM ( 2 cạnh đồng vị)
XÉt tam giác AMD và tam giác AME
AD =AE ( Gt)
DM=EM ( CMT)
AM cạnh chung
=> tam giác AMD=AME ( c.c.c )
chúc bạn học tốt
cho tam giác ABC có AB=AC trên các cạnh AB vf AC lấy tương ứng 2 điểm D và E sao cho AD=AE gọi M là trung điểm của BC.
a. C/M DE//BC
b. tam giác MBD=tam giác MCE
c. tam giác AMD=tam giác AME
Cho ABC vuông tại A có AB < AC, Trên cạnh BC lấy điểm D sao cho BA = BD. Từ D kẻ DE BC (E AC), Đường thẳng DE cắt đường thẳng AB tại M. Chứng minh rằng
a) Tam giác ABE = Tam giác DBE
b) BE Vuông Góc AD
c) Tam giác MBC cân
a: Xét ΔBAE vuông tại A và ΔBDE vuông tại D co
BE chung
BA=BD
=>ΔBAE=ΔBDE
b: BA=BD
EA=ED
=>BE là trung trực của AD
c: Xét ΔBDM vuông tại D và ΔBAC vuông tại A có
BD=BA
góc B chung
=>ΔBDM=ΔBAC
=>BM=BC
=>ΔBMC cân tại B
`a,`
Xét `2 \Delta` vuông `ABE` và `DBE`:
`\text {BE chung}`
`\text {BA = BD (2 cạnh tương ứng)}`
`=> \Delta ABE = \Delta DBE (ch-cgv)`
`b,`
Gọi I là giao điểm của AD và BE
Vì `\Delta ABE = \Delta DBE (a)`
`->` $\widehat {ABE} = \widehat {DBE} (\text {2 góc tương ứng})$
Xét `\Delta ABI` và `\Delta DBI`:
`\text {BA = BD (gt)}`
$\widehat {ABI} = \widehat {DBI}$
`\text {BI chung}`
`=> \Delta ABI = \Delta DBI (c-g-c)`
`->` $\widehat {BIA} = \widehat {BID} (\text {2 cạnh tương ứng})$
Mà `2` góc này ở vị trí kề bù
`->` $\widehat {BIA} + \widehat {BID} = 180^0$
`->` $\widehat {BIA} = \widehat {BID} =$\(\dfrac{180}{2}=90^0\)
`-> \text {BI} \bot \text {AD}`
Mà `\text {I} \in \text {BE}`
`-> \text {BE} \bot \text{AD}`
`c,`
Vì `\Delta ABE = \Delta DBE (a)`
`-> \text {AE = DE (2 cạnh tương ứng)}`
Xét `\Delta AEM` và `\Delta DEC`:
`\text {AE = DE}`
$\widehat {AEM} = \widehat {DEC} (\text {2 góc đối đỉnh})$
$\widehat {MAE} = \widehat {CDE} (=90^0)$
`=> \Delta AEM = \Delta DEC (cgv-gn)`
`-> \text {AM = DC (2 cạnh tương ứng)}`
Ta có: \(\left\{{}\begin{matrix}\text{BM = AM + AB}\\\text{BC = BD + DC}\end{matrix}\right.\)
Mà \(\left\{{}\begin{matrix}\text{BA = BD}\\\text{AM = DC}\end{matrix}\right.\)
`-> \text {BM = BC}`
Xét `\Delta MBC`:
`\text {BM = BC}`
`-> \Delta MBC` cân tại B.
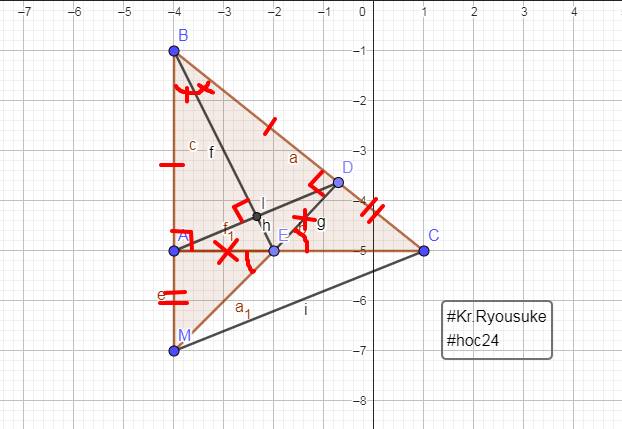
Cho tam giác ABC cân , AB = AC . Trên cạnh AC lấy điểm D và trên tia AB lấy E ( B nằm giữa A và E ) sao cho BE=CD. Nối D với E cắt BC ở M. Chứng Minh : M là trung điểm của DE
Cho tam giác ABC có AB=12,AC=16,BC=20 .
a) Chứng minh tam giác ABC là tam giác vuông;
b) Trên cạnh AB lấy điểm D sao cho BD = 4 .Từ D kẻ DE//BC (E∈AC).
Tính DE,EC.
c) Tìm vị trí điểm D trên cạnh AB sao cho BD+EC=DE.
Cho tam giác ABC vuông tại A (AB < AC). Trên cạnh AC lấy điểm D sao cho AB = AD. Trên tia đối của tia AB lấy điểm E sao cho AC = AE a) chứng minh tam giác ABC = tam giác ADE b) gọi M , N lần lượt là trung điểm của BC và DE , chứng minh AM = AN c) tính số đo của góc MAN
a: Xét ΔABC vuông tại A và ΔADE vuông tại A có
AB=AD
AC=AE
Do đó: ΔABC=ΔADE
a: Xét ΔABC vuông tại A và ΔADE vuông tại A có
AB=AD
AC=AE
Do đó: ΔABC=ΔADE
b: AM=ED/2
AN=BC/2
mà ED=BC
nên AM=AN
Cho tam giác ABC cân tại A . Vẽ AM vuông góc với BC ( M thuộc BC )
a) Chứng minh tam giác ABM = tam giác ACM
b) trên cạnh AB lấy điểm D , trên cạnh AC lấy điểm E sao cho AD = AE . Chứng minh tam giác ABE = tam giác ACD và DE song song với BC
c) Gọi I là giao điểm của BE và CD . Chứng minh AI là tia phân giác của góc BAC
a: Xét ΔABM vuông tại M và ΔACM vuông tại M có
AB=AC
AM chung
Do đó: ΔABM=ΔACM
b: Xét ΔABE và ΔACD có
AB=AC
\(\widehat{BAE}\) chung
AE=AD
Do đó: ΔABE=ΔACD
Xét ΔABC có \(\dfrac{AD}{AB}=\dfrac{AE}{AC}\)
nên DE//BC
c: Ta có: AD+DB=AB
AE+EC=AC
mà AD=AE và AB=AC
nên DB=EC
Xét ΔDBC và ΔECB có
DB=EC
\(\widehat{DBC}=\widehat{ECB}\)
BC chung
Do đó: ΔDBC=ΔECB
=>\(\widehat{DCB}=\widehat{EBC}\)
=>\(\widehat{IBC}=\widehat{ICB}\)
=>ΔIBC cân tại I
Xét ΔAIB và ΔAIC có
AI chung
IB=IC
AB=AC
Do đó: ΔAIB=ΔAIC
=>\(\widehat{BAI}=\widehat{CAI}\)
=>AI là phân giác của góc BAC
cho tam giác ABC có AB=AC trên các cạnh AB vf AC lấy tương ứng 2 điểm D và E sao cho AD=AE gọi M là trung điểm của BC.
a. C/M DE//BC
b. tam giác MBD=tam giác MCE
c. tam giác AMD=tam giác AME