Cho α + β = 90 0 , câu nào sau đây là đúng?
A. sin α = sin β
B. tan α = cos β cos α
C. sin 2 α + cos 2 α = 1
D. tan α . c o t α = 2 2
Tìm đẳng thức đúng
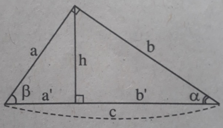
A. sin α = sin β B. sin α = cos β
C. sin α = tg β D. sin α = cotg β
Cho biết 0≤α≤π20≤α≤π2 sao cho
sin3(α)+cos3(α)=1sin3(α)+cos3(α)=1
Và β=sin(α)+cos(α)β=sin(α)+cos(α)
a) Tính ∑α=07π2(sin−1(β)+α)∑α=07π2(sin−1(β)+α)
b) Chứng minh rằng số ββ thỏa đề bài là nghiệm của phương trình: β3−6β+5=0
a) Trong hình 44, hệ thức nào trong các hệ thức sau là đúng?
( A ) sin α = b c ( B ) cotg α = b c ( C ) tg α = a c ( D ) cotg α = a c
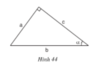
b) Trog hình 45, hệ thức nào trong các hệ thức sau không đúng ?
(A) sin2α + cos2α = 1
(B) sin α = cos β
(C) cos β = sin ( 90 ° – α )
(D) tg α = sin α cos α
a) Chọn C
b) Chọn C sai
- Vì đẳng thức đúng phải là: cos β = sin ( 90 ° - β )
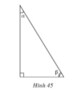
Trog hình 45, hệ thức nào trong các hệ thức sau không đúng ?
(A) sin2α + cos2α = 1
(B) sin α = cos β
(C) cos β = sin (90o – α)
D t g α = sin α cos α
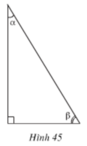
Chọn C sai
- Vì đẳng thức đúng phải là: cos β = sin(90o - β)
Tìm đẳng thức đúng:
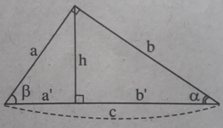
A. cos α = cos β B. cos α = tg β
C. cos α = cotg β D. cos α = sin β
Tìm đẳng thức đúng:
A. tg α = tg β B. tg α = cotg β
C. tg α = sin β D. tg α = cos β
Tìm đẳng thức đúng:
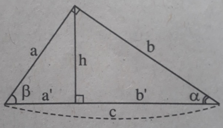
A. cotg α = tg β B. cotg α = cotg β
C. cotg α = cos β D. cotg α = sin β
Cho α , β thỏa mãn sin α + sin β = 2 2 ; cos α + cos β = 6 2 . Tính cos α - β .
A. cos α - β = 0
B. cos α - β = 2 2
C. cos α - β = 3 2
D. cos α - β = 1 2
CMR nếu α+β=90 độ thì sin α =cosβ, tan α= cot β
\(sin\alpha=cos\beta=\dfrac{AB}{BC}\)
\(tan\alpha=cot\beta=\dfrac{AB}{AC}\)
\(\alpha+\beta=90^o\)
\(\Rightarrow\beta=90^o-\alpha\)
Theo đề bài :
\(sin\alpha=cos\beta\)
\(\Rightarrow sin\alpha=cos\left(90^o-\alpha\right)\)
mà \(\alpha;90^o-\alpha\) là 2 góc phụ nhau
\(\Rightarrow cos\left(90^o-\alpha\right)=sin\alpha\left(dpcm\right)\)
Tương tự \(tan\alpha=cot\beta=cot\left(90^o-\alpha\right)\)
Cho sin α+β= \(\dfrac{1}{3}\),tanα=-2tanβ
Tính A= sin(α+\(\dfrac{3\pi}{8}\)).cos(α+\(\dfrac{\pi}{8}\))+sin(β-\(\dfrac{5\pi}{12}\)).sin(β-\(\dfrac{\pi}{12}\))
Để giải bài toán này, ta sẽ sử dụng các công thức và quy tắc trong lượng giác để tính toán.
Trước hết, ta có: sin(α+β) = sinα.cosβ + cosα.sinβ cos(α+β) = cosα.cosβ - sinα.sinβ
Đề bài cho α+β = 1313 và tanα = -2tanβ. Ta có thể suy ra các thông tin sau: tanα = -2tanβ => sinα/cosα = -2sinβ/cosβ => sinα.cosβ = -2sinβ.cosα
Bài toán yêu cầu tính A = sin(α+3π/8) . cos(α+π/8) + sin(β-5π/12) . sin(β-π/12)
Để tính A, ta sẽ thay các giá trị đã biết vào công thức trên:
A = sin(α+3π/8) . cos(α+π/8) + sin(β-5π/12) . sin(β-π/12) = (sinα . cos(3π/8) + cosα . sin(3π/8)) . (cosα . cos(π/8) - sinα . sin(π/8)) + (sinβ . cos(5π/12) - cosβ . sin(5π/12)) . (cosβ . cos(π/12) + sinβ . sin(π/12)) = (sinα . cos(3π/8) + cosα . sin(3π/8)) . (cosα . cos(π/8) - sinα . sin(π/8)) + (sinβ . cos(5π/12) - cosβ . sin(5π/12)) . (cosβ . cos(π/12) + sinβ . sin(π/12)) = (sinα . cos(3π/8) + cosα . sin(3π/8)) . (cosα . cos(π/8) - sinα . sin(π/8)) + (sinβ . cos(5π/12) - cosβ . sin(5π/12)) . (cosβ . cos(π/12) + sinβ . sin(π/12)) = (sinα . cos(3π/8) + cosα . sin(3π/8)) . (cosα . cos(π/8) - sinα . sin(π/8)) + (sinβ . cos(5π/12) - cosβ . sin(5π/12)) . (cosβ . cos(π/12) + sinβ . sin(π/12))
Tuy nhiên, để tính giá trị chính xác của A, cần biết thêm giá trị cụ thể của α và β. Trong câu hỏi của bạn, không có thông tin về α và β, do đó không thể tính toán giá trị của A.