Cho đường tròn (O, 15 cm) và đường tròn (O', 20 cm) cắt nhau tại M và N. Biết MN = 24 cm. O và O' nằm khác phía so với MN
c) Tam giác OMO' vuông
Phần tự luận
Nội dung câu hỏi 1
Cho đường tròn (O, 15 cm) và đường tròn (O', 20 cm) cắt nhau tại M và N. Biết MN = 24 cm. O và O' nằm khác phía so với MN
a) Chứng minh OO' vuông góc với MN
a) Xét đường tròn (O; 15 cm) có: OM = ON = 15 cm
⇒ O nằm trên đường trung trực của MN
Xét đường tròn (O'; 20 cm) có: O'M = O'N = 20 cm
⇒ O' nằm trên đường trung trực của MN
⇒ OO' là đường trung trực của MN hay OO' ⊥ MN
Cho đường tròn (O, 15 cm) và đường tròn (O', 20 cm) cắt nhau tại M và N. Biết MN = 24 cm. O và O' nằm khác phía so với MN
b) Tính độ dài đoạn OO'
Cho hai đường tròn (O; 20cm) và (O'; 15cm) cắt nhau tại A và B. Tính đoạn nối tâm OO', biết rằng AB = 24 cm. (Xét hai trường hợp: O và O' nằm khác phía đối với AB; O và O' nằm cùng phía đối với AB).
- Trường hợp 1: O và O' nằm khác phía đối với AB
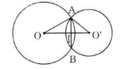
Gọi I là giao điểm của OO' và AB. Theo tính chất đường nối tâm ta có:
AB ⊥ OO' và AI = IB = 12
Áp dụng định lí Pitago, ta được:
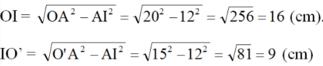
Vậy OO' = OI + IO' = 16 + 9 = 25 (cm)
- Trường hợp 2: O và O' nằm cùng phía đối với AB
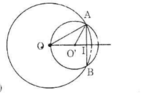
Tương tự như trường hợp 1, ta có:
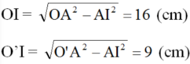
Vậy OO' = OI – O'I = 16 – 9 = 7 (cm).
Cho hai đường tròn (O; 20cm) và (O'; 15cm) cắt nhau tại A và B. Tính đoạn nối tâm OO', biết rằng AB = 24 cm. (Xét hai trường hợp: O và O' nằm khác phía đối với AB; O và O' nằm cùng phía đối với AB).
- Trường hợp 1: O và O' nằm khác phía đối với AB
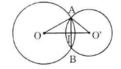
Gọi I là giao điểm của OO' và AB. Theo tính chất đường nối tâm ta có:
AB ⊥ OO' và AI = IB = 12
Áp dụng định lí Pitago, ta được:
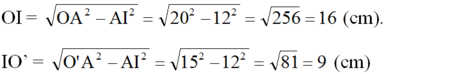
Vậy OO' = OI + IO' = 16 + 9 = 25 (cm)
- Trường hợp 2: O và O' nằm cùng phía đối với AB
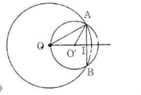
Tương tự như trường hợp 1, ta có:
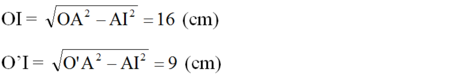
Vậy OO' = OI – O'I = 16 – 9 = 7 (cm).
Cho hai đường tròn (O,20 cm) và (O',15 cam) cắt nhau tại A và B. Biết AB = 24 cam và O và O' nằm về hai phía so với dây cung AB. Vẽ đường kính AC của đường tròn (O) và đường kính AD của đường tròn (O')
A) chứng minh 3 điểm C,B,D thằng hàng
B) tính độ dài đoạn OO'
Bài này hơi khó , bạn tự vẽ hình với làm câu a) nhé 😅😅
b)
00' cắt AB tại H
\(\Rightarrow AH=\frac{AB}{2}=\frac{24}{2}=12\)
Áp đụng Pythagore cho tam giác vuông AOH
\(OH=\sqrt{\left(20^2-12^2\right)}=16\)
Pythagore ▲vuông O'AH Áp dụng Pythagore cho tam giác vuông O'AH
\(O'H=\sqrt{\left(15^2-12^2\right)}=9\)
\(\Rightarrow OO'=OH+O'H=16+9=25cm\)
Vậy : OO' dài 25cm
Cho đường tròn (O;R) có đường kính AB. Từ điểm C nằm ngoài (O) kẻ cát tuyến CNM vuông góc với AB tại H (H nằm giữa O và B); AC cắt đường tròn (O;R) tại điểm K khác A, hai dây MN và BK cắt nhau ở E
a) CM: tứ giác AHEK nội tiếp đường tròn
b) Qua N kẻ đường thẳng vuông góc với AC cắt tia MK tại F. Chứng minh: tam giác NKF cân
cho tam giác ABC có đỉnh C nằm ngoài đường tròn(O) tâm O đường kính AB. Biết cạnh CA cắt đường tròn (O) tại điểm D khác , cạnh CB cắt đường tròn (O) tại điểm E khác B. Gọi H là giao điểm của AE và BD.
1/ cm tam giác ABD là tam giác vuông. Cm CH vuông góc với AB.
2/ Gọi F là trung điểm của đoạn CH. Cm DF là tiếp tuyến của đường tròn (O).
1) Xét (O) có
ΔDAB nội tiếp đường tròn (O)(Vì D,A,B∈(O))
mà AB là đường kính của (O)(gt)
nên ΔDAB vuông tại D(Định lí)
⇒BD⊥AD tại D
hay BD⊥AC
Xét (O) có
ΔEAB nội tiếp đường tròn(E,A,B∈(O))
mà AB là đường kính(gt)
nên ΔEAB vuông tại E(Định lí)
⇒AE⊥EB tại E
hay AE⊥BC tại E
Xét ΔCAB có
BD là đường cao ứng với cạnh AC(cmt)
AE là đường cao ứng với cạnh BC(cmt)
BD\(\cap\)AE={H}
Do đó: H là trực tâm của ΔCAB(Tính chất ba đường cao của tam giác)
⇔CH là đường cao ứng với cạnh AB
hay CH⊥AB(đpcm)
cho đường tròn (o) đường kính AB.Đường thẳng d vuông góc với AB tại I và cắt đường tròn (o) tại P và Q (I nằm giữa O và B).M là ddiemr bất kỳ nằm trên d(M nằm ngoài (o).Các tia AM và BM cắt đường tròn (o) lần lượt tại C và D.Đương thẳng CD và AB cắt nhau tại K,đường thẳng AD và BC cắt nhau tại H
a,cm tứ giác ACHI nội tiếp được trong một đường tròn
b,cm tam giác OCI đồng dạng OKC
a,Xét tứ giác ACHI có: góc ACB = 90o (góc nội tiếp chắn nửa đường tròn)
góc HIA = 90o (gt)
=> tổng hai góc này =180o mà đỉnh C và I lại nằm ở vị trí đối nhau => tứ giác ACHI là tứ giác nội tiếp đường tròn đường kính AH (đpcm)
Cho 2 đường tròn (O; 20 cm) và (O'; 15 cm) cắt nhau tại hai điểm M và N . Gọi I là giao điểm của MN và OO'
a, CM OO' vuông góc với MN
b, Cho MN = 24cm , Tính độ dài đth MI
c, Tính độ dài đoạn OO' . CM O'M là tiếp tuyến của đường tròn (O)