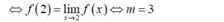Với giá trị thực nào của tham số c thì hàm số f x = − cx + 1 , khi x < 2 3 , khi x = 2 c 2 x 2 + 2 , khi x > 2 liên tục trái tại 2.
A. − 1 2 3 2 , 1 2 3 2
B. 1 2
C. -1
D. 0
Cho hàm số f(x) = a x 2 + bx + c đồ thị như hình. Hỏi với những giá trị nào của tham số thực m thì phương trình |f(x)| = m có đúng 4 nghiệm phân biệt.
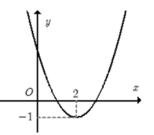
A. 0 < m < 1.
B. m > 3.
C. m = −1, m = 3.
D. −1 < m < m 0 .
Cho hàm số f(x) = a x 2 + bx + c đồ thị như hình. Hỏi với những giá trị nào của tham số thực mm thì phương trình f(|x|) – 1 = m có đúng 3 nghiệm phân biệt.
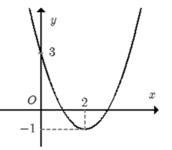
A. m = 3.
B. m > 3.
C. m = 2.
D. −2 < m < 2.
Cho hàm số f ( x ) = x - m 2 x + 8 với m là tham số thực. Giả sử m0 là giá trị dương của tham số m để hàm số có giá trị nhỏ nhất trên đoạn [0;3] bằng -3. Giá trị m0 thuộc khoảng nào trong các khoảng cho dưới đây?
A. (2;5)
B. (1;4)
C. (6;9)
D. (20;25)
Cho hàm số y = f ( x ) = a x 3 + b x 2 + c x + d với a, b, c, d là các số thực, có đồ thị như hình bên.
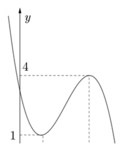
Có bao nhiêu giá trị nguyên của tham số m để phương trình f e x 2 = m có ba nghiệm phân biệt?
A. Vô số.
B. 3.
C. 1.
D. 2.
Cho hàm số y= f(x) xác định trên R và có đồ thị như hình bên. Hỏi với những giá trị nào của tham số thực m thì phương trình f ( x ) = m có đúng hai nghiệm phân biệt.
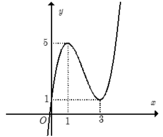
A.0< m< 1 .
B. m> 5.
C.m= 1; m= 5
D.0< m< 1; m> 5
+ Ta có y = f ( x ) = f ( x ) , f ( x ) ≥ 0 - f ( x ) , f ( x ) < 0 . Từ đó suy ra cách vẽ đồ thị hàm số (C) như sau:
- Giữ nguyên đồ thị y= f (x) phía trên trục hoành.
- Lấy đối xứng phần đồ thị y= f(x) phía dưới trục hoành qua trục hoành ( bỏ phần dưới ).
Kết hợp hai phần ta được đồ thị hàm số y = f ( x ) như hình vẽ.
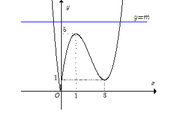
Phương trình f ( x ) = m là phương trình hoành độ giao điểm của đồ thị hàm số y = f ( x ) và đường thẳng
y= m (cùng phương với trục hoành).
Dựa vào đồ thị, ta có ycbt
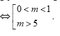
Chọn D.
Cho hàm số y=f(x) là hàm đa thức với hệ số thực. Hình vẽ bên dưới là một phần đồ thị của hai hàm số: y=f(x) và y=f'(x)
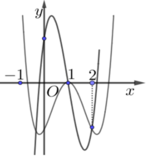
Tập các giá trị của tham số m để phương trình f ( x ) = m e x có hai nghiệm phân biệt trên [0;2] là nửa khoảng [a;b). Tổng a+b gần nhất với giá trị nào sau đây?
A. -0.81
B. -0.54
C. -0.27
D. 0.27
Cho hàm số f(x) = x4 - 2x2 + m - 1 (với m là tham số thực). Tìm tất cả các giá trị của tham số m để giá trị nhỏ nhất của hàm số g(x) = \(\left|f\left(x\right)\right|\) trên đoạn [0;2] bằng 2020.
\(f'\left(x\right)=4x^3-4x=0\Rightarrow\left[{}\begin{matrix}x=0\\x=1\\x=-1\end{matrix}\right.\)
Để \(g\left(x\right)_{min}>0\Rightarrow f\left(x\right)=0\) vô nghiệm trên đoạn đã cho
\(\Rightarrow\left[{}\begin{matrix}-m< -2\\-m>7\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}m>2\\m< -7\end{matrix}\right.\)
\(g\left(0\right)=\left|m-1\right|\) ; \(g\left(1\right)=\left|m-2\right|\) ; \(g\left(2\right)=\left|m+7\right|\)
Khi đó \(g\left(x\right)_{min}=min\left\{g\left(0\right);g\left(1\right);g\left(2\right)\right\}=min\left\{\left|m-2\right|;\left|m+7\right|\right\}\)
TH1: \(g\left(x\right)_{min}=g\left(0\right)\Leftrightarrow\left\{{}\begin{matrix}\left|m-2\right|\le\left|m+7\right|\\\left|m-2\right|=2020\\\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m\ge\dfrac{5}{2}\\\left|m-2\right|=2020\end{matrix}\right.\) \(\Rightarrow m=2022\)
TH2: \(g\left(x\right)_{min}=g\left(2\right)\Leftrightarrow\left\{{}\begin{matrix}\left|m+7\right|\le\left|m-2\right|\\\left|m+7\right|=2020\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}m\le\dfrac{5}{2}\\\left|m+7\right|=2020\end{matrix}\right.\) \(\Rightarrow m=-2027\)
Với giá trị thực nào của tham số m thì hàm số ![]() có cực trị ?
có cực trị ?
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Cho hàm số f ( x ) = x 2 - x - 2 x - 2 ; x ≠ 2 m ; x = 2 . Với giá trị nào của tham số m thì hàm số đã cho liên tục tại điểm x m = 2 ?
A. m = 3
B. m = -3
C. m = -1
D. m = 1
Chọn A.
- Ta có: f(2) = m.
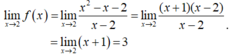
→ Hàm số liên tục tại điểm x = 2.