Các câu hỏi tương tự
Cho hàm số f(x) a
x
2
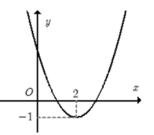
+ bx + c đồ thị như hình. Hỏi với những giá trị nào của tham số thực mm thì phương trình f(|x|) – 1 m có đúng 3 nghiệm phân biệt. A. m 3. B. m 3. C. m 2. D. −2 m 2.
Đọc tiếp
Cho hàm số f(x) = a x 2 + bx + c đồ thị như hình. Hỏi với những giá trị nào của tham số thực mm thì phương trình f(|x|) – 1 = m có đúng 3 nghiệm phân biệt.
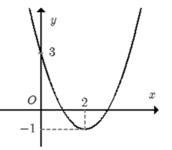
A. m = 3.
B. m > 3.
C. m = 2.
D. −2 < m < 2.
Cho hàm số f(x) a
x
2
+ bx + c đồ thị như hình bên dưới. Hỏi với những giá trị nào của tham số m thì phương trình |f(x)| − 1 m có đúng 2 nghiệm phân biệt. A.
m
≥
0
m
−
1
B. ...
Đọc tiếp
Cho hàm số f(x) = a x 2 + bx + c đồ thị như hình bên dưới. Hỏi với những giá trị nào của tham số m thì phương trình |f(x)| − 1 = m có đúng 2 nghiệm phân biệt.
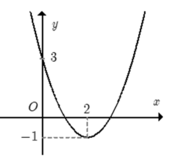
A. m ≥ 0 m = − 1
B. m > 0 m = − 1
C. m ≥ -1
D. m ≥ 0
Cho hàm số y = f(x) có bảng biến thiên như sau:
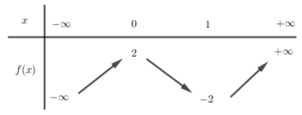
Với giá trị nào của tham số m thì phương trình |f(x) − 1| = m có bốn nghiệm phân biệt.
A. m = 1.
B. 1 < m < 3.
C. 0 < m < 1.
D. m ≥ 3.
3: cho hàm số f(x)=ax^2+bx+c có tọa độ đỉnh (2;-1) và có giá trị nhỏ nhất khi là -1 khi x=2
Tìm tất cả các giá trị thực của tham số m để phương trình |f(2017x-2018)-2|=m có đúng 3 nghiệm.
Câu 29: Cho hàm số y= f(x)= ax^2 + bx+c có đồ thị như hình vẽ bên.( dưới bình luận)
Có bao nhiêu giá trị nguyên m để phương trình
f^2(|x|)+(m- 2019) f (|x|)+m– 2020 =0 có 6 nghiệm
phân biệt
Em cần gấp ạ !!!!
Cho hàm số F(x) = (m + 1)x2 - 2mx + m - 2 (m là tham số). a) Tìm m để phương trình f(x) = 0 có hai nghiệm trái dấu? b) Tìm m để bất phương trình f(x) < 0 có một nghiệm đúng với mọi x.
Cho f(x)=x^2 -2(m-2)x+m+10. Định m để:
a. Phương trình f(x)=0 có một nghiệm x= 1 và tính nghiệm kia
b. Phương trình f(x)=0 có nghiệm kép. Tính nghiệm kép đó.
c. Tìm m để phương trình f(x)=0 có 2 nghiệm âm phân biệt.
d. Tìm m để f(x)<0 có nghiệm đúng với mọi xϵR
a) Số giá trị nguyên của tham số m thuộc (-5;5) để phuong trình x2+2mx+m2+m-3 =0 có 2 nghiệm phân biệt
b)Với giá trị nào của m thì nhị thức bậc nhất f(x)=mx-3 luôn âm với mọi x
Với giá trị nào của tham số m thì phương trình \(\left(m^2-1\right)x+m^2-2m-3=0\) vô nghiệm ?
A. \(m=1\) B. \(m=-1\) C. \(m=-2\) D. \(m=-3\)