Cho hình vẽ, trong đó DE // BC, AD = 12, DB = 18, CE = 30. Độ dài AC bằng:
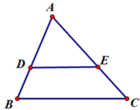
A. 20
B. 18 25
C. 50
D. 45
Cho hình vẽ, trong đó DE // BC, AE = 12, DB = 18, CA = 36. Độ dài AB bằng:
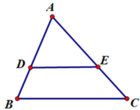
A. 30
B. 36
C. 25
D. 27
Vì DE // BC, theo định lý Ta-lét ta có
A D D B = A E E C ⇔ A D 18 = 12 36 − 12 ⇔ A D 18 = 12 24
=> AD = 18.12 24 = 9 cm
Nên AB = AD + DB = 9 + 18 = 27 cm
Đáp án: D
Câu 5 : Tổng các nghiệm của phương trình l2x-3l=2-x
A. \(\dfrac{2}{3}\)
B. \(\dfrac{8}{3}\)
C. \(\dfrac{5}{3}\)
D. 1
Câu 6: Cho △ABC có D,E lần lượt nằm trên các cạnh AB,AC sao cho DE//BC;DB =18,CE =30. Độ dài AC bằng
A.45
B.50
C.20
D.\(\dfrac{18}{25}\)
Câu 7 :một hình thang có đáy nhỏ là 9cm,chiều cao là 4 cm ,diện tích là 50cm2 .Đáy lớn là
A.15cm
B.18cm
C.25cm
D.16cm
Câu 8 : cho △ A'B'C'và △ABC có Â' =Â . Để △A'B'C'∼ △ABC cần thêm điều kiện là
A.\(\dfrac{A'B'}{AB}=\dfrac{BC}{B'C'}\)
B. \(\dfrac{B'C'}{BC}=\dfrac{AC}{A'C'}\)
C. \(\dfrac{A'B'}{BA}=\dfrac{C'A'}{CA}\)
D . \(\dfrac{A'B'}{AB}=\dfrac{B'C'}{BC}\)
Câu 9: điều kiện xác định của phương trình \(\dfrac{1}{x+2}+3=\dfrac{3-x}{x+2}\) là
A. x≠-3
B. x≠3
C. x≠-2
D. x≠2
C. Câu 10 :Tập nghiệm của phương trình \(\dfrac{x^2+3x}{x}=0\) là
A. S={0}
B.S={-3}
C.S={0;-3}
D.S=R
Câu 5: B
Câu 6: A
Câu 7: C
Câu 8: D
Câu 9:A
Câu 10: D
GIÚP MÌNH VỚI MÌNH ĐANG CẦN GẤP!!! TRÌNH BÀY CÁC BƯỚC C/M NHÉ!
Câu 13: Cho hình thang ABCD (BC // AD) có C=3D
Câu 14: Cho hình thang cân ABCD có BC = 3cm. Đường chéo DB vuông góc với cạnh bên BC; DB là tia phân giác của góc D. Khi đó độ dài DC bằng? Câu 15: Cho tam giác ABC vuông ở A, AB 6cm; AC=8cm. Gọi M, N lần lượt là trung điểm của AB và AC. Khi đó độ dài MN bằng?
Câu 16: Cho tam giác ABC có chu vi bằng 48cm. Ba đường trung tuyến AD; BE; CF. Khi đó chu vi của tam giác DEF bằng?
Câu 17: Cho hình bình hành ABCD có A-B=50. Khi đó góc D có số đo là?
Câu 18: Cho hình vẽ bên, biết AD=24cm; BE= 32cm. Khi đó độ dài của CH bằng?
Câu 19: Trong các câu sau, câu nào Sai?Hình bình hành có 2 góc có số đo là?
Câu 20: Cho hình bình hành ABCD có A=120 độ; AB=8cm. Gọi I là trung điểm của CD, biết AI=4cm, khi đó độ dài của đường chéo AC bằng?
Câu 13: Cho hình thang ABCD (BC // AD) có C=3D
.Câu 14: Cho hình thang cân ABCD có BC = 3cm. Đường chéo DB vuông góc với cạnh bên BC; DB là tia phân giác của góc D. Khi đó độ dài DC bằng? .Câu 15: Cho tam giác ABC vuông ở A, AB 6cm; AC=8cm. Gọi M, N lần lượt là trung điểm của AB và AC. Khi đó độ dài MN bằng?Câu 16: Cho tam giác ABC có chu vi bằng 48cm. Ba đường trung tuyến AD; BE; CF. Khi đó chu vi của tam giác DEF bằng?.Câu 17: Cho hình bình hành ABCD có A-B=50. Khi đó góc D có số đo là?.Câu 18: Cho hình vẽ bên, biết AD=24cm; BE= 32cm. Khi đó độ dài của CH bằng? .Câu 19: Trong các câu sau, câu nào Sai?Hình bình hành có 2 góc có số đo là? .Câu 20: Cho hình bình hành ABCD có A=120 độ; AB=8cm. Gọi I là trung điểm của CD, biết AI=4cm, khi đó độ dài của đường chéo AC bằng?1 Tìm x
Bài 2.cho tam giác ADE có AD = 5cm. Kéo dài AD thêm 1 đoạn DB=3cm .từ B vex tia song song với DE cắt AE tại C. biết AE-EC =3cm. tính AE, EC,AC
bài 3: cho hình thang ABCD. lấy I trên AD k trên BC sao cho IK // AB .cmr: AI/AD = BK/BC
bài 4 : Nếu 1 đthẳng ko đi qua các đỉnh của tam giác ABC và cắt các đthẳng BC,CA, AB theo thứ tự A', B', C'. cmr: AB'/B'C . CA'/A'B .BC'/C'A =1
giúp mik đi các proooo
Cho hình thang ABCD trong đó D thuộc AB; E thuộc AC; DE//BC; biết AD=18cm, DB=12cm; AE=30cm. Tính độ dài AC
Cho tam giác ABC có AB = 18 cm, AC = 12 cm, BC = 9 cm. Trên tia đối của tia CB lấy điểm D sao cho CD = 3 cm. Qua D kẻ đường thẳng song song với AB cắt tia AC tại E. Gọi F là giao điểm của AD và BE. Tính: a) Độ dài CE, DE
Xét ΔCAB và ΔCED có
\(\widehat{CAB}=\widehat{CED}\)(hai góc so le trong, DE//AB)
\(\widehat{ACB}=\widehat{ECD}\)(hai góc đối đỉnh)
Do đó: ΔCAB đồng dạng với ΔCED
=>\(\dfrac{CA}{CE}=\dfrac{AB}{ED}=\dfrac{CB}{CD}\)
=>\(\dfrac{12}{CE}=\dfrac{18}{ED}=\dfrac{9}{3}=3\)
=>\(CE=\dfrac{12}{3}=4\left(cm\right);ED=\dfrac{18}{3}=6\left(cm\right)\)
cho tam giác abc có góc a bằng 90 độ, góc c bằng 30 độ. điểm d thuộc cạnh ac sao cho góc abd bằng 20 độ. so sánh độ dài các cạnh ba, db, bc, ad, dc
nhanh lên nhé
cho ΔABC vuông tại A có AB=6cm, AC=8cm. AD là tia phân giác của ∠BAC( D∈BC)
a) tính tỉ số \(\dfrac{BD}{DC}\)và độ dài đoạn thẳng BC, DB, DC
b) kẻ DE⊥AB. Tính độ dài DE, AE và diện tích tứ giác AEDC
c) gọi O là giao điểm AD và CE. Qua O kẻ đg thẳng // AC cắt BC và AB lần lượt tại M, N. C/m: OM=ON
a: BC=10cm
Xét ΔABC có AD là phân giác
nên BD/CD=AB/AC=3/4
=>BD/3=CD/4
Áp dụng tính chất của dãy tỉ số bằng nhau,ta được:
\(\dfrac{BD}{3}=\dfrac{CD}{4}=\dfrac{BD+CD}{3+4}=\dfrac{10}{7}\)
Do đó: BD=30/7(cm); CD=40/7(cm)
b: Xét ΔABC có DE//AC
nên DE/AC=BD/BC
=>\(\dfrac{DE}{8}=\dfrac{30}{7}:10=\dfrac{3}{7}\)
=>DE=24/7(cm)