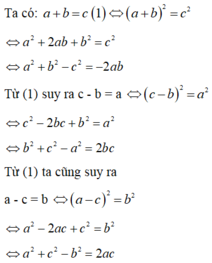\(ab+bc+ca=0\)

=>   \(\frac{ab+bc+ca}{abc}=0\)

=>  \(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=0\)

Đặt:  \(\frac{1}{a}=x;\)\(\frac{1}{b}=y;\)\(\frac{1}{c}=z\)

Ta có:   \(x+y+z=0\)

=>  \(x^3+y^3+z^3=3xyz\)  (tự c/m, ko c/m đc ib)

hay  \(\frac{1}{a^3}+\frac{1}{b^3}+\frac{1}{c^3}=\frac{3}{abc}\)

\(B=\frac{bc}{a^2}+\frac{ca}{b^2}+\frac{ab}{c^2}=\frac{abc}{a^3}+\frac{abc}{b^3}+\frac{abc}{c^3}=abc.\left(\frac{1}{a^3}+\frac{1}{b^3}+\frac{1}{c^3}\right)\)

     \(=abc.\frac{3}{abc}=3\)

thanks

Sai đề rồi nha bạn! 

Đề:  Cho  \(a,b,c>0\)  thỏa mãn  \(a^2+b^2+c^2=\frac{5}{3}.\)  Chứng minh rằng:  \(\frac{1}{a}+\frac{1}{b}-\frac{1}{c}<\frac{1}{abc}\)

Lời giải:

Với mọi  \(a,b,c\in R\)  thì ta luôn có:

\(a^2+b^2+c^2\ge2bc+2ca-2ab\)  \(\left(\text{*}\right)\) 

Ta cần chứng minh  \(\left(\text{*}\right)\)  là bất đẳng thức đúng!

Thật vậy,  từ  \(\left(\text{*}\right)\)  \(\Leftrightarrow\)  \(a^2+b^2+c^2+2ab-2bc-2ca\ge0\)

                             \(\Leftrightarrow\)  \(\left(a+b-c\right)^2\ge0\)  \(\left(\text{**}\right)\)

Bất đẳng thức  \(\left(\text{**}\right)\)  hiển nhiên đúng với mọi  \(a,b,c\) , mà các phép biến đổi trên tương đương 

Do đó, bất đẳng thức  \(\left(\text{*}\right)\)  được chứng minh.

Xảy ra đẳng thức trên khi và chỉ khi  \(a+b=c\)

Mặt khác,  \(a^2+b^2+c^2=\frac{5}{3}\)  (theo giả thiết)

Mà  \(\frac{5}{3}=1\frac{2}{3}<2\)

\(\Rightarrow\)  \(a^2+b^2+c^2<2\)  \(\left(\text{***}\right)\)

Từ  \(\left(\text{*}\right)\) kết hợp với  \(\left(\text{***}\right)\), ta có thể viết 'kép' lại:  \(2bc+2ca-2ab\le a^2+b^2+c^2<2\)

Suy ra  \(2bc+2ca-2ab<2\)

Khi đó, vì  \(abc>0\) (do  \(a,b,c\) không âm) nên chia cả hai vế của bất đẳng trên cho  \(2abc\), ta được:

\(\frac{2bc+2ca-2ab}{2abc}<\frac{2}{2abc}\)

\(\Leftrightarrow\)  \(\frac{1}{a}+\frac{1}{b}-\frac{1}{c}<\frac{1}{abc}\)

Vậy, với  \(a,b,c\)  là các số thực dương thỏa mãn điều kiện  \(a^2+b^2+c^2=\frac{5}{3}\)  thì ta luôn chứng minh được:

\(\frac{1}{a}+\frac{1}{b}-\frac{1}{c}<\frac{1}{abc}\)

Ta có: a+b+c=0

nên a+b=-c

Ta có: \(a^2-b^2-c^2\)

\(=a^2-\left(b^2+c^2\right)\)

\(=a^2-\left[\left(b+c\right)^2-2bc\right]\)

\(=a^2-\left(b+c\right)^2+2bc\)

\(=\left(a-b-c\right)\left(a+b+c\right)+2bc\)

\(=2bc\)

Ta có: \(b^2-c^2-a^2\)

\(=b^2-\left(c^2+a^2\right)\)

\(=b^2-\left[\left(c+a\right)^2-2ca\right]\)

\(=b^2-\left(c+a\right)^2+2ca\)

\(=\left(b-c-a\right)\left(b+c+a\right)+2ca\)

\(=2ac\)

Ta có: \(c^2-a^2-b^2\)

\(=c^2-\left(a^2+b^2\right)\)

\(=c^2-\left[\left(a+b\right)^2-2ab\right]\)

\(=c^2-\left(a+b\right)^2+2ab\)

\(=\left(c-a-b\right)\left(c+a+b\right)+2ab\)

\(=2ab\)

Ta có: \(M=\dfrac{a^2}{a^2-b^2-c^2}+\dfrac{b^2}{b^2-c^2-a^2}+\dfrac{c^2}{c^2-a^2-b^2}\)

\(=\dfrac{a^2}{2bc}+\dfrac{b^2}{2ac}+\dfrac{c^2}{2ab}\)

\(=\dfrac{a^3+b^3+c^3}{2abc}\)

Ta có: \(a^3+b^3+c^3\)

\(=\left(a+b\right)^3+c^3-3ab\left(a+b\right)\)

\(=\left(a+b+c\right)\left(a^2+2ab+b^2-ca-cb+c^2\right)-3ab\left(a+b\right)\)

\(=-3ab\left(a+b\right)\)

Thay \(a^3+b^3+c^3=-3ab\left(a+b\right)\) vào biểu thức \(=\dfrac{a^3+b^3+c^3}{2abc}\), ta được: 

\(M=\dfrac{-3ab\left(a+b\right)}{2abc}=\dfrac{-3\left(a+b\right)}{2c}\)

\(=\dfrac{-3\cdot\left(-c\right)}{2c}=\dfrac{3c}{2c}=\dfrac{3}{2}\)

Vậy: \(M=\dfrac{3}{2}\)

Câu hỏi của Hattory Heiji - Toán lớp 8 - Học toán với OnlineMath

tvbobnokb' n

iai

  ni;bv nn0

Do a+b+c= 0

<=> a+b= -c 

=> (a+b)²= c² 

Tương tự: (c+a)²= b², (c+b)²= a²   

Ta có: \(A=\frac{1}{b^2+c^2-a^2}+\frac{1}{c^2+a^2-b^2}+\frac{1}{a^2+b^2-c^2}\)

\(=\frac{1}{b^2+c^2-\left(b+c\right)^2}+\frac{1}{c^2+a^2-\left(c+a\right)^2}+\frac{1}{a^2+b^2-\left(a+b\right)^2}\)

\(=\frac{1}{-2bc}+\frac{1}{-2ca}+\frac{1}{-2ab}\)

\(=\frac{a+b+c}{-2abc}=0\)

\(a,\dfrac{a}{c}=\dfrac{c}{b}\Leftrightarrow\dfrac{a^2}{c^2}=\dfrac{c^2}{b^2}=\dfrac{a^2+c^2}{b^2+c^2}\left(1\right)\)

Mà \(\dfrac{a}{c}=\dfrac{c}{b}\Leftrightarrow ab=c^2\Leftrightarrow\dfrac{a}{b}=\dfrac{c^2}{b^2}\left(2\right)\)

Từ \(\left(1\right)\left(2\right)\tođpcm\)

\(b,\dfrac{a}{c}=\dfrac{c}{b}\Leftrightarrow ab=c^2\)

\(\Leftrightarrow\dfrac{b^2-a^2}{a^2+c^2}=\dfrac{\left(b-a\right)\left(b+a\right)}{a^2+ab}=\dfrac{\left(b-a\right)\left(b+a\right)}{a\left(a+b\right)}=\dfrac{b-a}{a}\left(đpcm\right)\)